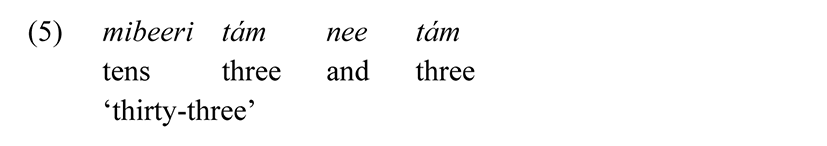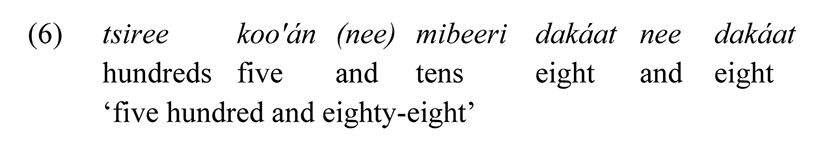1. Introduction
Numeral systems have long been of typological and historical interest across languages since Greenberg (1978) postulated 54 generalisations about the universal and near-universal numeral systems of world languages. Languages vary extensively in their numeral systems (Greenberg 1978, Donohue 2005, Beller & Bender 2008, Hammarström 2010, Comrie 2013, Bender & Beller 2014, Comrie 2020). The numeral system is universal since every language has numerals, but some languages have only indefinite numeracy; Other languages have number systems that express exact numeracy; Some other languages have only a restricted range of relatively small numbers; And others have fully productive counting systems that express exact numbers over a very large range (Comrie 2005, Xu et al. 2020). Additionally, a core property of numerals is that they can be derived ad infinitum (Hauser et al. 2002) by adding numbers and expanding the ‘number line’, which is an ordered list of sequential and increasing quantities, through a recursive process, according to the Packing Strategy (Hurford 2007), and this expansion gives rise to the number line (Calude & Verkerk 2016). The ad infinitum is cross-linguistically achieved through the counting system of numerals which involves diverse mathematical operations and grammatical processes (Greenberg 1978, Calude & Verkerk 2016, Sanusi & Yusuf 2018, Comrie 2020). These distinction of numeral systems are likely to be grounded in different cognitive capacities for judging numeracy; Thus, across-language variation in numeral systems may be understood in terms of a shared functional need to communicate precisely while using minimal cognitive resources (Xu et al. 2020). Additionally, different languages use diverse mechanisms in deriving up infinite numeral systems; which cross-linguistically include decimal, vigesimal, hybrid vigesimal-decimal and extended body part systems among others; with the decimal being the most common one (Comrie 2005).
The number is a core element of human knowledge (Spelke & Kinzler 2007). Counting forms an important component in the socio-economic activities of human beings in the sense that numerals are unavoidable facilities in their daily activities (like selling or buying, counting products, and counting possessions). Besides, numeracy appears to be a very important aspect of the linguistic system in the sense that it is an integral and inseparable part of the grammar of any language. There is no meaningful linguistic discourse in a language which makes no reference to quantity, size, time, distance, duration, and weight in definite numbers or numerals (Omachonu 2011). When counting, people make reference to time, the number of things or objects, distance, weight, age, height, and so forth. However, granting these significant roles, the indigenous numeral systems of the minority languages are at risk of endangerment or even extinction compared to other systems, even when the language itself is not endangered (Comrie 2005). The numeral systems of the majority of the world’s languages are in greater danger than the languages themselves. This vulnerability follows from the fact that language is not static, i.e., changes as a property of language are manifested in its contents, systems, and patterns, in particular numeral systems (McMahon 1994), which suffer the most following their vital roles as evidenced in their frequent use in the diverse everyday activities of human life. Thus, one of the aspects of grammar that is always identified as being in danger of endangerment is the use of the numeral system (Comrie 2005, 2006).
The endangerment of numeral systems has been experienced in larger languages, such as Japanese and Thai, where their numeral systems have been replaced by Chinese (Comrie 2005). Due to the escalating development, numerals have been subject to change, fatalities, and imperilment. As a result, the act of counting using indigenous numerals in a minority language is left to the community’s elders, while the younger generation often shies away from native counting and tends to prefer, adopt, or express numerals in dominant languages (Mreta 2011). This, in turn, results in the rapid replacement of the traditional numeral systems of the minority ethnic languages by those of the dominant languages. For instance, Mreta (2011) revealed that younger members of the community in the Chimalaba and Shimalila languages of Tanzania tend to give up their indigenous numeral systems and adopt borrowed ones. Mreta adds that indigenous numeral systems are particularly inclined to different kinds of sociolinguistic changes that arise through language contact, in which it is not unusual for the numeral system of the dominant language to replace the indigenous system of minority languages. Commonly, in a bilingual or multilingual community, as a result of language contact, the numerical system of the dominant language spoken in an area replaces the numeral systems of minority languages (Comrie 2006). In this article, “dominant language” refers to a language that is politically, socio-culturally, economically, educationally, technologically powerful, and prestigious. Swahili and at least English in Tanzania are the languages of schools, regional trade, and legal contracts. In the sociolinguistic context of Tanzania, Swahili as the dominant language has replaced (e.g., Chimalaba, Shimalila) and continues to replace the numeral systems of other ethnic community languages due to its penetration into the home domain. Swahilization is seen as another factor that gradually takes place by replacing the existing numeral terms through borrowing. In most languages, the numerals one to four or five are in use, while the higher ones have been replaced by the numeral systems of the dominant languages. For instance, Amaechi (2014) argues that young people and adults who have proficiency in their mother tongues hardly recite the conventional sequence of their traditional numerals; Hence, they borrow English numeral systems. This is in line with Comrie’s (2006) assertion that a community encountering another community with greater numeracy may well borrow the absent parts of its system from that other community, may also replace parts or all of the existing systems, and can also affect languages that come into contact even where there is no great difference in numeracy due to the cultural or commercial superiority of one group over the other. The same is happening between Swahili numeral systems and ethnic community languages in Tanzania.
While the survival chance of indigenous numerals in both minority and majority languages is in question, there is a need for documentation and description of numeracy (Comrie 2020). This paper attempts to examine the numeral systems in the four West-Rift Southern Cushitic languages. Southern Cushitic includes ethnic languages such as Dahalo (spoken in Kenya), Ma'a/Mbugu, Asax, Qwadza, Burunge, Alagwa, Gorwaa, and Iraqw (Mous 1993), of which Qwadza and Asax are extinct, possibly with their numeral systems neither documented nor described. The scope of this article is limited to the four West-Rift Southern Cushitic languages,1 namely Iraqw, Gorwaa, Alagwa, and Burunge, which are located in the West-Rift branch (Ehret 1980, Kießling 2000). According to Kießling’s (2000) classifications of West-Rift languages, Iraqw, Gorwaa, and Alagwa belong to the Northern West-Rift, while Burunge alone falls into the isolated group of the Southern West-Rift due to its distinctive phonological and morphological features (Kießling & Mous 2003) from the Northern West-Rift languages. Based on the geographical dispersion of native speakers, these languages are spoken in the Rift Valley of Tanzania, particularly in the Manyara, Arusha, and Dodoma regions. These languages are scantily documented and less described (each to a varied degree). This is based on the quality and quantity of the existing documented materials and described data for each language. Based on the number of speakers, Burunge, Alagwa, and Gorwaa depict a smaller minority number of speakers than Iraqw, with more than half a million native speakers, but this does not guarantee the survival of Iraqw numeracy.
Substantiating Comrie’s reasons for the greater vulnerability and endangerment of the numeral system than the language itself is imperative before the numeral systems of lesser documented and studied languages perish completely. In this vein, Comrie (2005) suggests that, given the present rate of language death in the world, it may no longer be possible to even approximate the range of possible numeral systems in natural languages or to assess the relative frequency of different types. Thus, this study aims to provide detailed descriptive analyses of the numeral systems of the four West-Rift Southern Cushitic languages, with a focus on the underived and derived cardinal numerals, ordinal numerals, distributive numerals, derivational processes, and some changes that have taken place in their numeracy.
2. Methods and Sources of Data
The qualitative data for the study was collected in Mbulu, Babati, Kondoa, and Chemba districts. One village in each district with a high concentration of native speakers was purposely selected. Elicitation, observations, and documentary reviews were used to generate the data for the study. Alagwa data were collected in Humai, Burunge in Pumpayi; Gorwaa data in Endanachan, and data for Iraqw in Gunyoda. Elicitation aimed to probe the counting knowledge of the speakers between ages 10–80+. This age range is important to examine the variation of knowledge and usage of indigenous numeral systems. Informants were asked to count through indigenous numeral words (from 1–1,000), to state their (date, months, and year) of birth using their mother tongue. Also, they were asked to read prepared figures using their mother tongue. These aimed to examine their knowledge and use of indigenous numeral systems. The researcher also employed the non-participant observation and purposively listened to the way people asked and negotiated prices of commodities. The researcher further asked sellers the price of things like cup of coffee, sugar, tin of charcoal, bunch of firewood, vegetables, using native language—my aim is to capture usage of numeracy in the spontaneous speech.
3. Numeracy in West Rift Southern Cushitic Languages
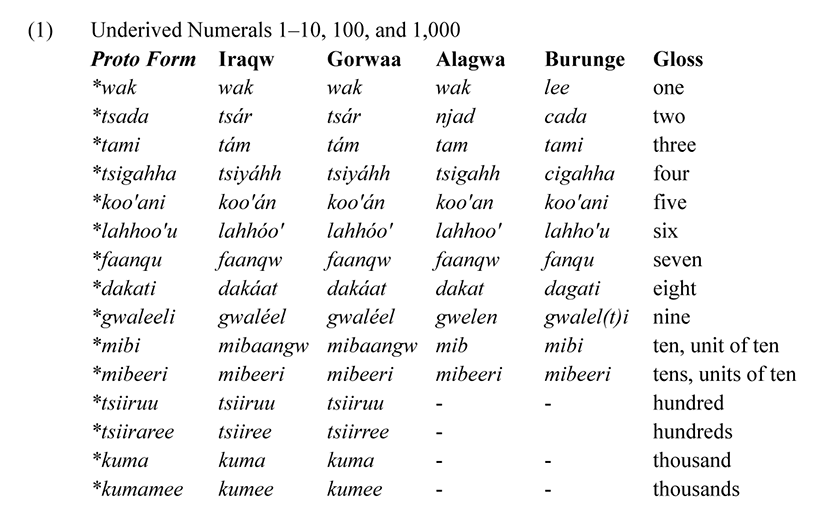
The study confines itself to the numeral system of the Iraqw, Gorwaa, Algwa, and Burunge. The counting starts from 1–1,000+ number words because the traditional counting rarely goes beyond one thousand. This is because people very rarely possess objects or things especially animals and farm produce that exceed more than a thousand. Sociocultural, economic, and commercial activities, employed a barter exchange system of farm products with animals, or other products like baskets, pots, etc. It is very rare for a person to own more than one thousand animals especially cattle, sheep, goats etc. Thus, for clear and systematic presentation, numerals of the four West-Rift subgroups of Southern Cushitic languages are categorised into primary and secondary as far as counting is limited from one to a thousand. Primary numerals refer to basic (core or underived) numerals which are morphologically monomorphemic (formed by a single morpheme) in nature, while the latter are the non-basic (derivatives) which are formed from basic numerals by a combination of basic numerals (1–10) through different mathematical operations, such as addition, multiplication, and a combination of both addition and multiplication processes.
Greenberg (1978) categorises the coding of numerals as atoms and syntagma, whereby the former are items which receive simple lexical expression (lower numerals) and the latter refer to forms derived from atoms (Winter 1992). Based on this, West-Rift languages, like other languages with unrestricted number systems, exhibit productive number systems formed through the combination of atoms and syntagma to obtain higher numerals.
In counting from one to a thousand in Iraqw, Gorwaa, Alagwa, and Burunge, basic numerals are underived, monomorphic, and are used for deriving the secondary numerals through some grammatical and mathematical (addition, multiplication, and combination of) processes. Basic numerals number words for 1–10 in the four languages. In Iraqw and Gorwaa, both 100 and 1,000 are morphologically basic and monomorphic numbers as they appear completely independent, and their bases contribute to developing other numerals of high sums. In Alagwa and Burunge, 100 and 1,000 are derivatives formed by the multiplication of base ten to another numeral unit as explained in the section of derivation through multiplication. Basic numeral systems with the proto forms for one through thousands are depicted in (1).
Reading from the data above, the numeral words from one to thousands are cognate words of Southern Cushitic origin for Iraqw and Gorwaa. However, Burunge uses a distinct form lee for ‘one’ while the other three languages maintain the proto form wak ‘one’. Alagwa maintains the cognate forms from one to ten, while Burunge has maintained two through ten. Nevertheless, they probably lost cognate words for hundred through thousands and thus they derive them through multiplication of base ten with unit ten. Tracing back to old numeracy, Alagwa uses derivatives mibeeri mib (10 × 10) for one hundred and mibeeri mib (awaa) mib (10 × 10 × 10) for one thousand. On the other hand, Burunge uses mibeeri mibi (10 × 10) for one hundred and mibeeri mibi mibi (10 × 10 × 10) ‘one thousand’. In both languages hundred and thousand are formed by multiples of ten with ten. However, in the modern numeral systems, Alagwa borrowed Swahili numeral words miyaa for ‘hundred(s)’, and elefu for ‘thousand(s)’, while contemporary Burunge uses a combination of Swahili miyaa and native word lee for ‘one hundred’ and the same for elefu lee for ‘one thousand’. The derived forms for hundred and thousand in Alagwa and Burunge are hardly found and remain only on the tongues of old people.
From phonological observation, one could see that Iraqw, Gorwaa, and Alagwa are characterised by final vowel loss of the proto form for numeral words for two to ten, as in dakáat, dakat ‘eight’, where in Iraqw and Gorwaa the loss of final vowel is compensated by internal vowel lengthening.
In Alagwa, the proto ejective /ts/ in *tsara is replaced with palatal obstruent /dʒ/ which associate with irregular prenasalization /ndʒad/, but in Burunge, /ts/ is replaced with palatal obstruent /tʃ/ while retaining the proto terminal vowel /tʃada/. Alagwa nasalizes final /l/ > /n/ as gwelen of proto from *gwaleeli which is associated with internal vowel reduction and loss of the terminal vowel while Burunge interchanges /l/ and /t/ for *gwaleeli as gwaleel(t)i as revealed in different sources of the numeral system.
Although Burunge at least maintains the final vowel of the proto form, yet, it experienced reduction or shortening of the internal vowels in*lahhoo'u > lahho'u, and *faanqu > fanqu as well as voicing of obstruent /k/ > /g/ in *dakati > dagati.
Iraqw and Gorwaa apart from loss of terminal vowels, they exhibit tonalisation except for wak ‘one’ and faangw ‘seven’, velar weakening in /g/ > /j/ in * tsigahha > tsiyáhh as well as dental lenition of /d/ > /r/ in *tsada > tsár. Other phonological processes are final glottalisation of mibeeri' in Gorwaa. There is reduction of reduplicated CV internal syllable of *tsiiraree ‘hundreds’ to tsiiree for Iraqw and internal vowel loss tsiirree for Gorwaa; while *kumamee becomes kumee in both languages.
Again, loss of terminal vowel of *mibi is replaced by lengthening of /a:/ and the addition of labialized velar nasal /ŋw/; hence, /miba:ŋw/. Gliding of the final back high vowel /u/ of */faanqu/ > /faanqw/ is exhibited in Iraqw, Gorwaa, and Alagwa.
In West-Rift languages, the creation of a derivative (syntagma) includes three constituents, namely atoms (monomorphemic), a base which is an existing atom used serially to derive larger numerals, and mathematical operations. Derived numeral terms comprise the vast majority of number words that are created from atoms (1–9) and base (10, 100, and 1,000) through different arithmetic operations, such as addition, multiplication, and both addition plus multiplication. For easy follow-up, secondary numerals are put into teens comprising numerals 11–19, crowns (for numerals 20, 30, 40, 50, 60, 70, 80, 90, and its running numbers 21–29, 31–29, 41–49, 51–59, 61–69, 71–79, 81–89, 91–99); and hundreds (100, 200, 300 ...) and thousands’ (1,000, 2,000, 3,000 ...) extensions.
The addition of two basic numerals derives 11–19 numerals. In the investigated Southern Cushitic languages, analysis revealed that numbers above ten are formed by adding lower number units to ten. The addition is expressed via conjunctive synonymous to the English conjunction ‘and’. Both Iraqw and Gorwaa use the conjunction nee ‘and’ while Alagwa and Burunge employ haa ‘and’. This is illustrated in examples in (2).
As can be seen from the above, the derivation of 11–19 takes only the addition of the cardinal basic numerals 1–9 to base ten. The order in the derivation of tens in these languages is strictly base ten plus atoms (1–9) of which ‘(10 + (and) 3 = 13)’ derive mibaa nee tám ‘thirteen’. Aside from the arithmetic process of addition, derivation subscribes to the phonological process. The former equally involves the elision of the final nasal sound in mibaangw ‘ten’. The additional sense is expressed by using overt conjunction nee and haa ‘and’ suggesting that one basic numeral and another basic result to secondary/non-basic numeral i.e., derivation involving the use of overt conjunction or addition of morpheme nee for Iraqw and Gorwaa, and haa for Alagwa and Burunge.
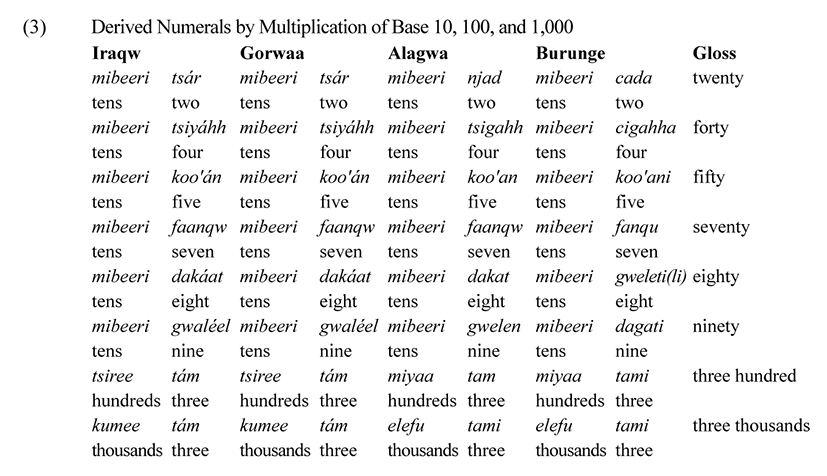
Multiplication in multiples of ten, hundred, and thousand are used to derive high sums. The multiplication operation is a technique used to say the numerals base ten, hundred, and thousand times a basic numeral (unit). The operation is conveyed in numeral terms consisting of a base ten, hundred, and thousand qualified by another numeral as in (3).
As can be seen from the above, high sums are obtained via multiplication of bases 10, 100, and 1,000 against another basic number. Given that West-Rift languages use a decimal system, the multiplication base is either a morphological derivation of the form for ten i.e., multiples of ten with basic numerals 1–9 derive 20, 30, 40, 50, 60, 70, 80, and 90. For instance, 10 × 2 = 20, 10 × 3 = 30 ... 10 × 9 = 90. This derivation process is applicable in the four languages. Multiples of hundred with basic numerals 2–9 derive 200, 300, 400, 500, 600, 700, 800, 900. For instance, 100 × 2 = 200, 100 × 4 = 400 ... 100 × 9 = 900. Multiples of thousand with basic numeral 2–10 derive 2,000, 3,000, 4,000, 5,000, 6,000, 7,000, 8,000, 9,000, and 10,000. For example, 1,000 × 5 = 5,000, 1,000 × 7 = 7,000, 1,000 × 10 =10,000, and so on to form indefinite and more complex high sums.
In Iraqw and Gorwaa numeral words tsiru for 100 and kuma for 1,000 appear completely as independent underived, but in Alagwa and Burunge, the older forms for 100 and 1,000 are derivatived by using base ten. For instance, in Burunge 100 is expressed as mibeeri mibi ‘lit. tens ten (10 × 10)’ and 1,000 is mibeeri mibi mibi ‘lit. tens ten ten (10 × 10 × 10)’ derivatives when traced back to the history of their counting. However, the modern counting systems employ Swahili number words miyaa and elefu lee for 100 and 1,000, respectively. The Alagwa old expression for 100 is mibeeri mib ‘tens ten (10 × 10)’ and 1,000 is mibeeri mib (awaa) mib ‘tens ten of ten (10 × 10 × 10)’. Thus, through multiplication, multiples of ten derive high sums 100 and 1,000, respectively. For all the four languages, the same operation for the extension of great numbers such as 100,000 (100,000 × 3) and 1,000,000 (1,000,000 × 5) are adopted from Swahili laki and mili'oni / miliyooni respectively, as in (4).
Based on the decimal base system, the numerals for 20, 30, 40, 50, 60, 70, 80, and 90 are derived from the corresponding atoms (2–9) through a series of a combination of multiplication and addition of base ten. These arithmetic operations and some grammatical processes derive the extension for 20–99 by using ten as in (5).
As can be observed in (5) the derivation involves a combination of multiplication of ten to basic numeral 3 (equals to 33); and then adding the products (33) to another basic unit/numeral 3 to form 33; hence, [(10 × 3) + 3 = 33].
For higher sums, for instance, the extension from 100–999, base hundred is multiplied to a basic numeral/unit, and add the product to the product of base ten (formed by multiples) and then adds to the basic unit/numeral. Schematically: (base hundred) × (basic numeral) + (base ten × basic numeral) + basic numeral as captured in (5) whereby 588 is [(100 × 5) + (10 × 8) + 8] = 588 as described in (6).
As can be read in (6) tsiree koo'án (nee) mibeeri dakáat nee dakáat, the conjunction morpheme (nee) ‘and’ that adjoins hundreds with tens is optional, while the nee ‘and’ that joins base ten to basic (lower) numeral is obligatory. The extension of thousands becomes more complex with a series of multiplication and addition of base thousand, hundred and ten with a basic numeral. As seen in (7), nee is optional for extension of thousands.
The above derivative arithmetically read as [(1,000 × 4) + (100 × 7) + (10 × 9) + 1] = 4,791. The plus sign is supposed to be represented by co-ordinating morpheme nee (Iraqw and Gorwaa) or haa (Alagwa and Burunge) ‘and’, but it is obligatorily used to connect the whole extension with a basic numeral. Thus, for numerals 20–99, addition and multiplication processes are most commonly used; and the order of derivation is strictly base-then-atom. This ordering conforms to the argument that cognitively, it is easier to make sense of a number if the larger portion of it comes first; Whereas the opposite order (atom-then-base) leaves the hearer in the dark till the last item is reached (Greenberg 1978).
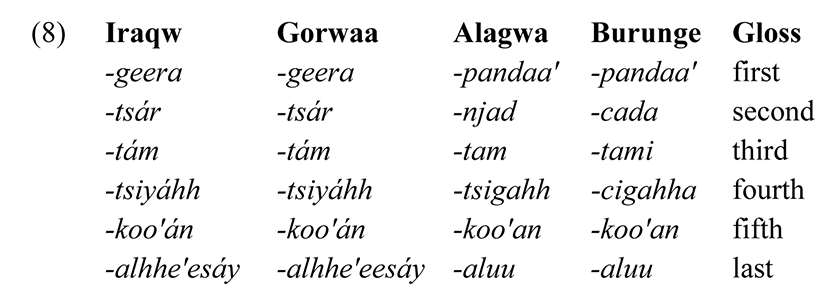
Ordinal numerals are used to identify ranks within a hierarchy with a view to situating a noun referent in a particular hierarchical position. Ordinals indicate the absolute rank where something occurs in a sequence. In the four languages, ordinal numerals are derived from the combination of a cardinal numeral and a noun. This category of the numeral expresses ordinals by blending a noun and the numeral expression, for instance, geera ‘the first, front’ for Iraqw and Gorwaa and pandaa' for Burunge and Alagwa. In other words, the numeral words wak and lee ‘one’ are not used in expressing the ordinal word for ‘first’. The words geera and pandaa' mean ‘face, front, first’ as depicted in (8).
As can be seen, only two independent ordinal numbers found in the lexicon of the languages, are not derived: geera or pandaa' ‘first, face, front’ and alhhe'eesáy or aluu ‘last, back’. In these four languages, ‘first’ is a suppletive derivationally independent of the cardinal numerals wak and lee ‘one’, respectively. For other numerals from two (2) upwards, the derivation process involves blending the noun either in construct case or followed by an independent noun suffix based on the gender of the noun that precedes the basic numeral.
The derivation process of ordinals in Iraqw involves placing the construct case suffix marked by final high tone on noun preceding the number. Also, the derivation employs independent noun suffixes oo for masculine (9), ar for feminine (10), and awa for neuter (11).
Unlike Iraqw, a Gorwaa noun preceding the number is not in construct form (realized by the high tone on the final vowel). The ordinal number is preceded by independent noun suffixes oo for masculine and neuter and ar for feminine as shown in (12) and (13).
However, Alagwa uses noun suffixes ta for feminine and ko for both masculine and neuter as demonstrated in examples (14) and (15).
However, it is unusual to use construct forms like, ?hiruú pandaa' ‘first person’; Hence, the independent noun suffixes ko and ta for the formation of ordinals are obligatory.
Burunge ordinals are preceded by independent suffixes da for feminine, while gu for masculine and neuter as in examples (16) and (17) depicted.
Gorwaa, Burunge, and Alagwa use one form of an independent noun suffix for both masculine and neuter nouns blended with basic numeral words to derive ordinals. In Iraqw, a noun preceding a basic numeral is normally in construct form (which is realised by a high tone mark on the final vowel of the noun) while in Gorwaa, Alagwa, and Burunge the derivation of ordinals does not employ the construct suffix. The independent noun suffixes oo, ar, awa (Iraqw), oo and ar (Gorwaa), ko, ta (Alagwa), da and gu (Burunge) are used to substitute the noun when the referent is known for both the speaker and hearer.
This type of numeral word in the four languages is derived from cardinal numerals through the morphophonological processes of reduplication. For the basic numerals (lower numbers) which are monomorphic, the tendency is total reduplication of numeral words. Derivation for high sums from ten upwards involves the partial reduplication of the basic (lower number) numeral as indicated in the examples (18).
As can be seen above, it is clear that the derivation of distributive numerals goes through either complete or total reduplications of the basic form. There is a reduction of tens, hundreds, and thousands in the reduplication process. For instance, mibeeri tsár tsár ‘twenty-two by two’ in actual sense means mibeeri tsár mibeeri tsár. Although the surface realization indicates partial reduplication, the underlying derivation shows total reduplication. Speakers tend to avoid redundancy of some units especially tens, hundreds, and thousands.
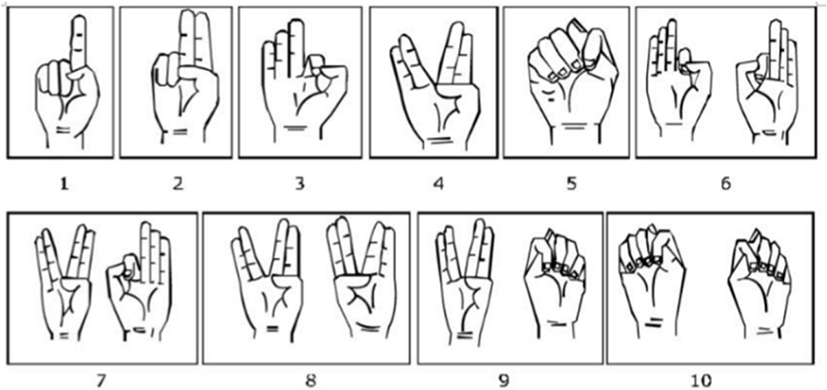
Southern Cushitic languages show the numbers 1–10 by gestures in line with the common East African System. For instance, 2 is formed by forefinger and middle finger brushing against each other and 3 by forefinger, middle finger, and ring finger (no movement), 4 is expressed by forefinger and middle finger as a pair separated by a V-shape from ring-finger and little finger, also as a pair; 5 is expressed by raised fist, often moving, 6 is formed by 3 + 3, 7 by adding 3 + 4, 8 by adding 4 + 4, 9 by adding 4 + 5, and 10 is formed by two fists hitting each other (Mous 2012). This is depicted in the sketch (Figure 1).
This knowledge of number gestures is currently in the last stages of disappearance among the speakers of these four languages. In the course of conducting this study, a large majority of youth in the communities could not make the signs used. For the most part, only very few old people can hardly recite these. The majority of the old members of these Southern Cushitic communities could not demonstrate this gesturing when asked to do so. Generally, counting by using fingers (number gestures) is extinct to the majority of the native speakers of these languages because the elders of the community do not use them when making reference to things or objects due to the influence of Swahili. Hence, knowledge of numerals has not been passed down to the young generations for several decades.
4. Current Status of Indigenous Numeracy
Children do not have knowledge of the indigenous counting system especially among the Burunge, Alagwa and to some extent Gorwaa, while in Iraqw, this situation is not prevalent because the majority can count from one through one thousand. In addition, in Alagwa and Burunge, indigenous numeral terms, mibeeri mib/mibi ‘tens ten’ for 100 is replaced by miyaa or miyaa lee ‘hundred’ and mibeeri mibi mibi/mibeeri mib awaa mib ‘tens ten ten or tens ten of ten’ for 1,000 is replaced by elefu or elefu lee ‘thousand’. However, some old members of the Alagwa and Burunge were able to recall the derived indigenous expression mibeer mib ‘tens ten’ for 100, and for 1,000 Alagwa uses a derived expression mibeeri mib awaa mib ‘tens ten of ten’. But speakers admitted that these expressions are no longer used; Instead they use miya and elefu/alfu. These four languages use loan Swahili expressions laki (laki lee for Burunge) for 100,000 and mili'oni (miliyooni lee) for 1,000,000. However, together with laki and mili'oni, the old Iraqw speakers have the derived indigenous expressions kumér tsiiru for a 100,000 (1,000 × 100) and kumér kuma (1,000 × 1,000) for a 1,000,000 which are infrequently or not used in spontaneous discourse. The desertion of the indigenous words is a sufficient indication that the speakers have alternative words which are definitely borrowed ones, to express and perform the same function. In this case the part of the numeral systems of the Alagwa and Burunge is replaced. These numeral words for hundred through thousand might have been replaced by Swahili due to long-term contact with Langi, Gogo, and Sandawe whereby Swahili serves as the lingua franca. This means that before this contact these languages had their numeracy for higher numbers.
This replacement cannot be explained by what Görlach (2007) referred to as three basic motives that may induce speakers of a language to borrow concepts from other languages as a gap in the numeral system of the recipient language, insufficiencies in the lexis of the recipient language and fashion or prestige. This is because these languages have their indigenous words to express 100 through 1,000, while Iraqw has words for 100,000 and 1,000,000. It can be said that the borrowing of Swahili words miya, and elefu/alfu for Alagwa and Burunge is not motivated to fill a gap; Instead they replaced the existing forms; Hence, foreign numeral words come to serve the same function as those replaced. This means that the borrowed Swahili numeral items do not introduce new terms in terms of function.
However, the Swahili numeral words laki for 100,000 and milioni for 1,000,000 instead fill the gap as a result of the insufficiencies in the lexis of the recipient languages Gorwaa, Algwa, and Burunge. This is in the same line with Görlach (2007) who asserts that insufficiencies of numeral lexis or the gap in one language especially for higher numbers motivate borrowing from a majority language. Regarding Iraqw, borrowing of laki and milioni for 100,000 and 1,000,000 respectively is for replacement because the language has its description for these numbers. Regarding the endangerment of indigenous counting systems, Comrie (2005, 2006) revealed many cases of languages that are not endangered, but still their number systems are endangered. Since language death results from social factors, Comrie adds that the numeracy is likely vulnerable to such social factors as language contact. A minority community encountering a majority community with a great numeracy tends to borrow the missing part of the system, whereby the four languages borrow the terms laki for 100,000 and miliyooni for 1,000,000 from Swahili. Even the Swahili has borrowed milioni for 1,000,000 from the English word ‘million’ to fill the missing expression for such a number; And even English borrowed it. As said herein, in a bilingual or multilingual context, it is not uncommon for the numeral terms of the dominant language(s) to supplant those of minority languages. Iraqw, Gorwaa, Alagwa, and Burunge, which are restricted to informal domains, co-exist with Swahili and English. That being the case, the Swahili and English languages and their numeracy enjoy high status since their numeracies are learned at school. Due to its status and functional load it has, Swahili numeracy penetrated and is continuously penetrating to the numeracy of ethnic languages through education, religion, trades, business, and so on. The movement of people from one place to another increases contact to the extent that no community in Tanzania is in isolation.
More seriously, some Burunge speakers have interchanged indigenous terms for eight and nine as well as for five and six. This mixing up for adjacent numeral terms is another indication of the loss of indigenous counting as shown in (19).
The substitution or interchange of the adjacent numeral terms is evident in Burunge, whereby the speakers tend to interchange numeral terms for eight and nine as well as for five and six. For instance, gwelel(t)i for ‘eight’ instead of ‘nine’ and dagati for ‘nine’ instead of eight. They also substitute numeral terms for five and six i.e., koo'ani ‘six’ instead of ‘five’ and lahhoo' as ‘five’ instead of ‘six’. However, in Kießling (1994) data koo'ani is ‘five’, lahho'u is ‘six’, and dagati is ‘eight’ and gwelel(t)i is ‘nine’ which are similar to the proto form. The substation or loss of higher cardinal numerals above five may be a result of the universal limit of the focus of human attention that the lowest four numerals refer to quantities that can be perceived (Cowan 2001); They appear in natural language much earlier than the higher ones; While the higher numerals are dependent on the knowledge of counting (Rutkowski 2003). Rutkowski explains this contrast as a result of the working memory’s limited capacity, which cognitivists argue is indeed four items.
Also, this implies that the frequent use of the lowest numerals 1–4 makes speakers more easily recall them than 5+ numerals. The observed substitution (mixing up) of these numeral terms is an indication of the loss of knowledge over indigenous numeral terms which might have been caused by the infrequent use of native terms in their everyday communication. This is in the same line with Hammarström (2004) who argues that frequency, with special attention to cognitive reference points, is a better explanation. As a result counting is done through other languages’ numeracy particularly Swahili’s. Parents admit that their children have Swahili and English numeral knowledge learned at school, mosque, and church. This in the long term may lead to the replacement of the whole system of the numerals, as in the case of Chimalaba whereby Swahili replaced all of the existing system (Mreta 2011). The reasons for preference of numeral systems of majority languages over minority languages may be cultural or commercial dominance of one group over the other, in this case Swahili against ethnic languages of Tanzania which are marginalized. The cultural and/or commercial dominance of Swahili as a national language, regional lingua franca, and language of instruction has resulted in its numeral systems being adopted by many ethnic languages though there is no great difference in numeracy of Swahili and Tanzanian ethnic community languages.
Since in Tanzania, ethnic community languages are placed lower in the hierarchy of usage, this paper focuses on the influence of Swahili on the use of Southern Cushitic numeral systems. It is revealed that Swahili numeral terms have won over the tongues of the majority of the speakers of ethnic community languages including the four Southern Cushitic languages than their indigenous numeral terms. This is evident among Burunge and Alagwa speakers whereby a majority of the speakers are found to have limited knowledge of their indigenous numeral terms; Some can at least count from one to five, some do not have knowledge, and very few can count from 1–90. This implies that in rare cases small number terms are used by speakers who know them. Practically, in terms of usage, the Swahili numeral terms replaced indigenous numeral terms, as even the older members are found using them frequently. For instance, in business centres, speakers ask price of commodities, order things and negotiate prices using Swahili or code mixing as in (20), (21), and (22) from Burunge and Alagwa. However, ethnic community languages’ numeral terms are opted when the speaker(s) communicates with a person of the same tongue or he/she wants to exclude outsiders.
Although Iraqw and Gorwaa speakers are revealed to count using indigenous numeral terms still Swahili’s influence is outstanding. The majority of the influenced groups are children and youngsters. This group does not have sufficient knowledge of indigenous numeral terms. Simple and underived indigenous numerals are more used in their daily communication than complex ones. Complex numbers which involve various arithmetic operations (addition, multiplication, and addition-multiplication) are infrequently or not used because they probably are difficult to recall. The infrequency tendency in the usage of derived numerals may result in their endangerment or loss as evidenced in Alagwa and Burunge speakers who have lost derived terms for hundred through thousand which are replaced by Swahili miyaa and elefu, respectively. The rule of thumb is that frequently used numbers tend to survive, such as the lower or basic numerals 1–9. Thus, the frequency of usage of numeral terms has a symmetric relation to their survival. In the spontaneous speech speakers tend to use borrowed numeracy, code mixing or switching.
Görlach (2007) postulated three basic motives that may induce speakers of a language to borrow lexical items from another language, namely gaps in the numeral systems of the recipient language, insufficiencies in the lexis of the recipient language and fashion or prestige. Based on Southern Cushitic speakers, the use of Swahili numeral terms is triggered by two things. One, the gap in their numeral systems which motivates speakers to fill it by adopting Swahili numeral terms. Gaps of great numerals like 100,000 and 1,000,000 triggered the borrowing from Swahili, a dominant language. Second, borrowing is also motivated by fashion and prestige. Since Swahili enjoys high status, some members have adopted and continuously use its numeral terms due to sheer ostentation, modernity, fashion and prestige. Using indigenous numeral terms may seem old-fashioned.
Moreover, the analysis has revealed heavy code-switching and borrowing of numeral terms among Burunge and Alagwa who have almost lost the knowledge over their indigenous numeral terms like miya koo'ani ‘five hundred’, and elefu cada ‘two hundred’. Swahili has replaced the existing forms that serve the same functions played by indigenous ones for such numerals as a 100 and a 1,000. This means that borrowed numeral terms do not introduce new terms except for great numbers such as a 100,000 and a 1,000,000. Thus, buying and selling in the market as well as any other use of numbers use the Swahili numeral terms.
Some reasons that make speakers lose knowledge and abandon or cease using their indigenous numeracy are: use of Swahili as a national language and a language of education, government forums health services, political/government meetings, primary court proceedings, business centres, and religious services etc. These put indigenous languages’ numeric systems in jeopardy. This is in line with Comrie (2005) who argues that indigenous numerals are even more endangered than other systems, even if the language itself is not. For instance, the Iraqw language is not endangered but its speakers prefer Swahili numerals over their traditional ones as evident when individuals count using Swahili terms.
Traditional knowledge of counting had been passed down from elders to the young generations consciously or unconsciously usually orally and informally, or through traditional games that involve counting things like mugú' ‘game of guessing the number of grains or pebbles hidden in hand’, gooxí ‘game with pebbles for children’, and takti ‘game with two rows of holes and pebbles in them’ in Iraqw. There is a great decline of traditional folklore and also indigenous games which involve counting using the mother tongue. These games are very significant in the development of child counting cognition, as well as in acquiring and comprehending indigenous numerals. The penetration of Swahili into the home domain is weakening and killing the intergenerational transmission of these games and other folklores by creating an opportunity to use Swahili numerals like its other aspects, hence, dwindling the traditional numeral system. In turn, traditional counting has been left to the older members of the community while younger members tend to shy away from the use of indigenous numeral terms and prefer the Swahili and/or English numerals as a result Swahili numeracy has replaced and is continuously replacing the numeral systems of ethnic community languages. This claim is supported by Comrie (2013), who demonstrated that classical Mayan was influenced by a dominant language’s numerical systems after the conquest led to many indigenous languages adopting the Spanish numerical ciento 100 and decimal systems for the expression of the hundreds.
Early schooling age between 4/5 (in rural areas) exposes many children to Swahili and English numeracy, before mastering the mother tongue as well as indigenous numerals. This goes hand in hand with parents who insist and assist their child to learn and master the counting system used at school, which is Swahili and English. Parents insist on Swahili and English counting because they are taught in schools. Parents are happy to see their children count in languages used as the medium of instruction. This seems to be the main killer of knowledge of indigenous numeral terms. The forbidding/prohibiting of indigenous languages at schools leads to a limited time of acquiring indigenous numerals, since before joining schools children can speak and count through indigenous terms, but the knowledge starts to cease as they join the formal education. In fact, children learn more easily in their traditional counting system than in second and foreign languages. Matang & Owens (2014) argue that students who learned their traditional counting systems in their own languages spent less time and made fewer mistakes in accomplishing each assignment than those who were taught in a second and a foreign language; Unfortunately indigenous languages are not favoured and prohibited to be used at school in Tanzania. Restriction of ethnic languages in school settings seems to decline the children’s morale in learning and use of their indigenous languages as well as indigenous numerals. Since Swahili and English numeracy are tested, evaluated and graded as a requirement children put their efforts into acquiring and learning them so as to perform well.
Furthermore, due to the interaction with other language communities, trading and transactions are conducted through Swahili, a national language and the regional lingua franca. The increasing/growth and establishment of business centres (kiosks, tea/coffee cafes, monthly and weekly markets) in rural interiors where prices and exchange of goods as well as products are in most cases negotiated in Swahili. This results in the adoption of its numeracy. To support this, Powell & McCarthy (2010) argue that the decline of indigenous numerals is motivated by commercial issues whereby due to trade with Arabs, Indians, and Europeans, African numerical systems were replaced by Arabic numerals although Africans have their own numeral systems, with almost every language having a unique way of expressing numbers that is standardized. The systems existed before contact with foreigners were replaced by foreign systems, as is the case with Swahili, which has replaced the Chimalaba numeral system (Mreta 2011), and indigenous terms for one hundred and one thousand in both Alagwa and Burunge.
Given the negative sentiments towards their native language, some speakers have the tendency to shy away and be introverted when using indigenous numerals, thinking that they are old-fashioned. This is triggered by modernisation and fashion. Youngsters want to view themselves in the global worldview. This and other factors bring about a decline in knowledge and use of indigenous numeral terms of minority languages, thus, its vulnerability to endangerment and/or extinction. If today’s speakers do not have sufficient knowledge of their native numerals then what will be happening in 50 years to come, when this group is older. Obviously, if deliberate measures are not taken, then indigenous numeral systems will disappear. With time, Swahili numeral systems will be borrowed even for simple/basic numerals due to intense contact with Swahili through education, religious services, business, migration, traveling and others.
5. Conclusion
This article has examined cardinal, ordinal, distributive numerals, and current usage of numerals of the four West-Rift Southern Cushitic languages spoken in Tanzania. In understanding the vitality of indigenous numeracy, the paper has also examined the speakers’ knowledge over, and the trend of usage of indigenous numerals in their everyday activities. West-Rift Southern Cushitic languages numerals are based on the decimal numerical system. Cardinal numerals are categorised into underived and derived forms. Morphologically, the underived are simple, monomorphic/monolexeme words, since none of them can be analyzed as a result of a regular morphological or morphosyntactic process. Underived lower numerals include 1–9, and monomorphemic bases 10, 100, and 1,000. However, 100 mibeeri mib(i) and 1,000 mibeeri mib(i) mib(i) in Alagwa and Burunge are derived from base ten. These derived forms are very rarely used by the older member, whereby speakers borrowed the Swahili numeral miiya for 100 and elefu for 1,000. It seems that the two languages lost the West-Rift proto form *tsiru and *kuma; Hence, they started deriving 100 and 1,000, and latter shift to Swahili underived terms. The base 10 plays a role in the formation of teens, 100 in the formation of hundreds and 1,000 in the formation of thousands. Numbers from 100,000+ are formed through derivation using base thousands. For instance, in Iraqw, 100,000 is kumer tsiru ‘lit. thousands hundred’ (1,000 × 100) and 1,000,000 is kumer kum(a) ‘lit. thousands thousand’ (1,000 × 1,000), but speakers shifted to Swahili loan-number words laki and milioni which are monomorphemic, hence, simple to utter than the derived phrase. The numeracy of these languages conforms to most numerals of the world’s languages in terms of the morphology and derivation processes of higher numbers.
On the other hand, derived or secondary numerals are morphologically compound and complex phrases which are formed through mathematical operations working in parallel with some morphological and phonological processes. Compound numerals (teens) 11–19 are derived by the addition of base ten to lower numerals 1–9 by using the conjunction morpheme nee (Iraqw, Gorwaa) or haa (Alagwa, Burunge), whereby in Iraqw, the numeral word for base ten which precede a word for the lower number is marked with construct case suffix. Thus, the derivation of compound numerals 11–19 follows strictly the order base ten plus atom; (10 + 1 = 11 ... 10 + 9 = 19). Furthermore, complex numerals are formed by a series of mathematical operations such as multiplication (b × n), and a more complex system uses both addition and multiplication applied to the base [(b × n) + m] which go parallel with some grammatical processes. This order implies that counting starts with larger to smaller number. Multiplication involves decimal base ten (20–90), hundred (200–900), and thousand (2,000–10,000+), whereby the extension of tens [24 = (10 × 2) + 4], hundreds [333 = (100 × 3) + (10 × 3) + 3], and thousands [2,567 = (1,000 × 2) + (100 × 5) + (10 × 6) + 7] are derived through the application of series of multiplications of bases and additions of lower numbers. The derivation of the more complex higher numerals strictly follows the order (base × atom + m) in which mathematical operations work together with the morpheme nee or haa ‘and’.
The ordinals are derived from the cardinal numerals by the use of the noun expressions. The derivation of ordinals for ‘first’ do not use wak or lee ‘one’: instead it employs nouns geera or pandaa' ‘first, front, face’; While ordinal for ‘last’ is alhhe'eesay ‘last’ or aluu ‘back’, respectively. Iraqw and Gorwaa use geera and alhhe'eesay, while Alagwa and Burunge use pandaa' and aluu. However, in the derivation of ordinals from two and above, the cardinal numerals are blended to noun referents. The derivation of distributive numerals morphologically requires full reduplication of a numeral word in the four languages.
While this study made an assessment of the vitality of numeral systems of the four West-Rift Southern Cushitic languages, it has generated information that suffices to show how the indigenous numeral systems of minority languages are susceptible to endangerment and/or extinction resulting from language change due to the long contact with socio-culturally and commercially dominant and prestigious languages. In a contact context, the numerals of the dominant languages are borrowed to replace the indigenous ones or to fill the gap for higher numbers. The Swahilization process also has replaced and is gradually replacing the indigenous numeral terms; As a result the younger members of the community tend to embrace borrowed ones as noted in the languages under investigation. Other factors accelerating the vulnerability are intermarriages; speakers’ negative attitude towards their language; decline in the domain of usage of ethnic languages; lack of written literacy and materials. Moreover, an early schooling age contributes to the loss, whereby parents insist on and assist their children in learning the number systems taught at school. The deterioration of folklores and traditional games which involve counting also triggers the loss of knowledge and usage of indigenous numeracy. The loss of indigenous number words and adoption of loan numbers lead to change, replacement, and/or loss of lexicon in the respective semantic field. Given that numbers are the core vocabulary of the language, thus, deliberate documentation, description, and revitalization are needed to preserve indigenous numeral systems of the minority languages other than these four West-Rift Southern Cushitic languages.