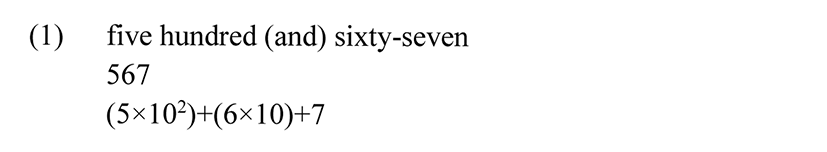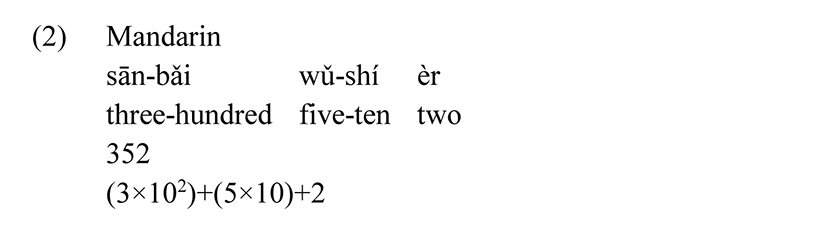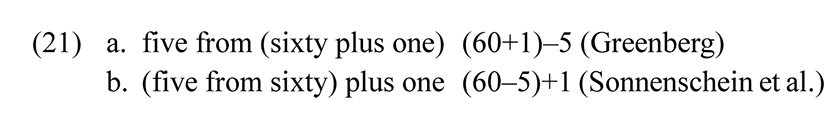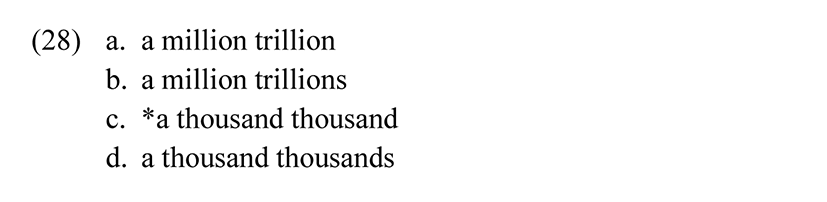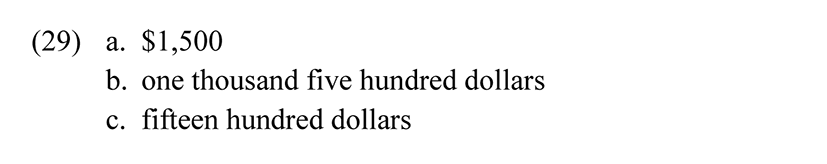Revisiting Greenberg’s “Generalizations about Numeral Systems” (1978)^*

In Modern English, as illustrated in (1), the order of the addends is consistently decreasing, and this is fact the most widely attested order crosslinguistically; it is illustrated in (2) from Mandarin Chinese to give an example from a completely different language family.

Although much rarer, there are some languages that consistently use the inverse, increasing ordering, as in (3) from Standard Malagasy (Rajaonarimanana 2001: 67, slightly modified).

This order is also one of the possibilities available to Arabic, although it is not the usual ordering found in the modern language (for which see below); Ali (2013: 71-72) gives examples noting: “This style is frequently used in classical texts or by those imitating the classical style”.

However, some languages make use of a mixture of decreasing and increasing order, with German being perhaps the most famous example of a language that uses basically decreasing order but places the units before the tens, as in (4).

This is also the usual order in Modern Arabic (Ali 2013: 66-71).

The question arises: Are there constraints on the possible combinations of descending and ascending orders? Greenberg proposed two such constraints:

Generalization 26: If in a language, in any sum the smaller addend precedes the larger, then the same order holds for all smaller numbers expressed by addition.

Generalization 27: If in a language, in any sum the larger addend precedes the smaller, then the same order holds for all larger numbers expressed by addition.

These two generalizations are in a sense mirror images of each other, and can be combined into a single generalization that if a language combines descending and ascending orders, then it will use ascending order for lower numbers and descending order for higher numbers, although the cut-off point between the two patterns may vary cross-linguistically, and there may be an intermediate area where both are possible. More specifically, the generalizations allow languages like German with the order hundreds—units—tens, but would disallow the inverse order tens—units—hundreds.

As it happens, languages of Europe and nearby areas present a rich variety of variations on the theme of consistency with this universal, i.e., languages with basically descending order but ascending order for some set of lower numbers (with different cut-off points). German, as illustrated in (4) and again in (5), has the cut-off point at 100.

Although English-speakers are typically unaware consciously of the fact, English also combines the two orders, although the cut-off point here is at 20, as illustrated in (6).

Romance languages typically have a cut-off point within the teens, either between 16 and 17, as in Italian example (7), or between 15 and 16, as in Spanish example (8).

The Insular Celtic languages provide, in their traditional vigesimal (base 20, “score”) systems, evidence for various cut-off points around 60, although different sources are not always entirely in agreement on the precise details. For Manx, Kewley Draskau (2008: 106-107) gives only the order Unit—Score through 59, but describes the order Score—Unit as occurring “usually” from 61 up, as in (9).

For Scottish Gaelic, Calder (1923: 127), describing the standard language, gives only the order Unit—Score for 21-23, 31-33, 41-42, both orders for 50 (alongside the alternative ‘half-hundred’ construction), and only the order Score—Unit for 70 and the higher twenties 130, 150, 170 and 190. Oftedal (1956: 228-229), describing a spoken variety of Scottish Gaelic, gives the order Unit—Score for 21, 22, 30 and 32, but the order Score—Unit for 41, 51 (alongside the ‘half-hundred and one’ construction, with ‘half-hundred’ as the only form cited for 50), and 73 (in 4573), suggesting a cut-off point in this dialect at 40. For Welsh, Bowen & Rhys Jones (1960: 109) give only the order Unit—Score below 60 but both orders above 60 with the recommendation “use the bigger number first”, i.e., Score—Unit; Hurford’s extensive study of numerals in the Welsh translation of the Bible from 1620 finds only Unit—Score below 60, both orders above 60 (Hurford 1975: 154-163). So where a variety has both descending and ascending order, it is always the case that ascending order is used for lower numbers, descending order for higher numbers, though there may also be an “intermediate” zone (which may extend to the upper limits of the system) where both orders are possible.

In his discussion of Generalizations 26-27, Greenberg noted that he was aware of “just one” exception, namely Trumai, where 3 is expressed as (2+1) but 6 is expressed as (1+5),⁵ and likewise for 7-9 and 11-14 (e.g., 11 as (1+10)). A sample of relevant forms from Greenberg’s source, Steinen (1894: 541-542), with the analysis implied by Greenberg’s remarks, is given in (10); square brackets identify instances where Greenberg’s implied analysis is questionable.

These forms can be compared by those given by Guirardello (1999: 46-48), a modern linguistic study of the Trumai language.⁶ Note that some alternative forms have been omitted from (10) and (11), and that the present-day speakers did not form numerals above 10 in Trumai.

The numeral 3 shows agreement across the two sources, but while the first component is recognized as identical to 2 by present-day speakers, the second is not recognized as 1, or indeed as anything—it would thus be a cranberry morph. Since Trumai has no demonstrable linguistic relatives, there is no possibility of attempting an etymology based on comparative material. One can speculate on possible etymologies (?big-two, ?beside-two), but this is pure speculation, and at most one can say that there is no evidence for Greenberg’s analysis (2+1). The modern form for 6 does not contain any explicit reference to 5, but is literally something like ‘[one] hand finger crosses’, i.e., one crosses over to one finger of the second hand in finger-counting; reference to 5 is at best derived from the fact that the first hand has five fingers. The form given by Steinen is apparently a contracted variant of this. The second component of the form for 11 given by Steinen is related to the word for ‘foot’, pits’ in the modern language recorded by Guirardello, so the overall form is probably a contraction of something like ‘one finger crossing to the foot’, so again the concept 10 is at best derived, from the fact that one has ten fingers, and beyond ten has to start counting the toes. Steinen’s form for 11 bears no resemblance to that given for 10, whose first component is the item recorded by Guirardello (1999: 48) as yupun ‘all’, i.e., one has crossed over to all five fingers of the second hand. In sum, further details of Trumai, which were not available to Greenberg in 1978, suggest that there is no motivation for analyzing Trumai in a way that makes it an exception to Generalizations 26-27.

However, we do now know of one clear counterexample to these generalizations, from Sakalava Malagasy, and more specifically its Nosy Be dialect.⁷ It will be recalled (see (3)) that Standard Malagasy has consistently ascending order. Sakalava Malagasy differs from this in placing the tens before the units, as noted explicitly by Dahl (1968: 14), who gives the example (12).

This is a clear counterexample, and therefore raises the question whether there is any validity to the pair of Generalizations 26-27. One might counter that this is only one exception, so that the generalizations would still stand as near-universals. But it must be borne in mind that this exception can only arise in a language that has basically ascending order, and that basically ascending order is much rarer than basically descending order in the world’s languages. There are therefore far more opportunities for languages to combine ascending order at the bottom with basically descending order than for languages to combine descending order at the bottom with basically ascending order. And simple statistical testing will not work, since the different languages that combine basically descending order with ascending order at the bottom are not all independent of one another. Unless and until a valid statistical test can be carried out, there is a real possibility that Generalizations 26-27 are simply spurious.

Note, however, that a more general conclusion drawn by Greenberg (1978) in his discussion of Generalizations 26-27 does still seem to hold up, namely that there is a strong crosslinguistic preference for descending order, perhaps motivated by the fact that descending order facilitates identification of the ballpark value of the numerical expression, especially for higher numbers, by giving its numerically largest component first.

Another possible counterexample to Generalizations 26-27 is presented by the sixteenth-century Toba data in (13) (Bárcena n.d.: 226),⁸ where the expression for 9 has the larger addend before the smaller, but the expression for 10 has the smaller addend before the larger.

However, generalizations drawn from data as in (13) need to be treated with some caution. The problem is that they derive from unique sources for limited attestation of numerals that are no longer current in the modern language (for Toba: Harriet Manelis Klein, p.c.). While there is no reason to doubt the genuineness of the data in (13), there is no reason to assume that the versions given in the source were the only versions possible in usage at the time, rather than for instance both orders Larger—Smaller and Smaller—Larger being possible for both numerals, in the absence of an explicit statement by the author that alternatives are excluded. In other words, even if we have complete confidence in what the author says, we cannot be sure how to interpret what they do not say.

A second caveat is that in such examples we are often dealing with isolated linguistic formations rather than general patterns that are either fully productive or at least define a substantial series of numeral expressions, such as the teens in English or the combinations of tens and units in English or German. If a given formation is used for only a very limited number of numerals—Trumai (10c) on Greenberg’s analysis, for instance, would be a single instance of this construction—then it may well be that speakers simply learn the whole for as a unit, especially if the formation is even partially opaque. Sakalava Malagasy is therefore particularly valuable in that it clearly establishes a productive pattern that goes against Generalizations 26-27.

While addition, multiplication, and exponentiation form the cornerstones of nearly all numeral systems that extend to relatively high numbers, there are some other arithmetic processes that are used occasionally, including subtraction, as illustrated in Latin example (14), where both 18 and 19 are expressed by subtraction from 20, e.g., 20–2=18.

It will be useful to introduce some terminology to refer to the different elements in the equation y–z=x; y will be referred to as the minuend and z as the subtrahend; the result is usually referred to as the difference, but for our purposes it will be more helpful to refer to it as the target, since it is the target number that the linguistic expression denotes. In example (14a), the target is 18, the minuend is 20, and the subtrahend is 2.

Greenberg (1978: 15) proposes the following constraint on minuends:

Generalization 14: Every minuend is a base of the system or a multiple of the base.

Since Latin has a decimal system, with base 10, and the minuend in (14) is 20, a multiple of the base (20=2×10), Latin is consistent with this generalization, as are most instances of subtraction in numeral systems of the world’s languages.

Greenberg discussed three counterexamples to Generalization 14. The first two deal with restricted sets of expressions rather than a productive process, but are still worth examining, as they do throw light on the precise nature of the arithmetic processes involved. The first is from Arikara, as presented by Wied (1841: 472). Relevant forms are given in (15), along with the forms for the current language from Parks (2009).

Once one makes allowance for Wied’s somewhat impressionistic transcription, there is close agreement between the two sets of data through 10; for the teens, however, the systems diverge. The forms of interest are those for 7 and 9 in both columns and for 11 as given by Wied. In each case, the expression contains a first component that is identical or almost identical to the expression for the next higher number, followed by an element that we can refer to as -waana on the basis of the current form. The formation is thus reasonably transparent: -waana is an instruction to subtract 1 from the number that is expressed by the first component, to arrive at the target value, i.e., 8–1=7, 10–1=9, and in Wied’s documentation 12–1=11. Now, Arikara overall has a vigesimal numeral system (Parks 2009), but since the teens are formed by adding to the expression for 10, 10 serves as a lower base within the system for the range 11-19. Even though Wied does not list other teens, the expression for 12, pitchóchin, is apparently composed of píttcho ‘two’ and a contraction of nochén ‘ten’, so 10 presumably served as a lower base in the system documented by Wied too. If we interpret the expressions for 7, 9 and 11 as subtractive, then that for 9 is unproblematic for Generalization 14, since the minuend is 10, but the expressions for 7 and 11 are problematic, since neither 8 nor 12 is a base of the system or a multiple of a base.

It should, however, be noted that the formative -waana is not the word for ‘one’, and one might therefore argue that these formations are not strictly speaking subtractive, but might be given some alternative interpretation, e.g., along the lines of ‘the item before (sc. in counting)’. If Generalization 14 is interpreted as strictly referring to subtraction, then the Arikara forms in -waana do not fall under the generalization and therefore neither instantiate nor counterexemplify it. However, there is clearly an intuition that goes beyond subtraction in the literal sense and seems implied by Greenberg’s use of the term “subtraction” for expressions that do not literally include any reference to subtraction of a particular subtrahend. What unites subtraction and examples like those from Arikara is that a numeral is identified by first identifying a higher numeral and then counting down from that higher numeral, in the case of Arikara counting down by just 1. We may then refer to the set of constructions that count down as “counting down” constructions. If we then generalize the term “minuend” to denote the number from which one counts down, whether this is expressed literally as subtraction or not, then we match Greenberg’s intuition that there is something unusual about the Arikara expressions for 7 and (in Wied’s data) 11, namely that they count down from a number value that is not a base of the system.

One might speculate on whether there are still constraints on possible minuends in this extended sense, and I will return below to some relevant empirical facts when I consider the Colonial Valley Zapotec numeral system. One possibility worth pursuing is that the minuend must be a “salient” number value in the culture, but validating this would of course involve checking whether 8 and 12 are or were indeed salient number values in Arikara, as otherwise there is a danger of the claim becoming circular, declaring by fiat that any minuend is culturally salient. But there are clear instances of numbers that are salient in a given culture though not a base in the numeral system, e.g., 12 in English, which is not a base or a multiple of a base in the language’s decimal numeral system, but nonetheless receives a special secondary lexical designation as dozen.

Before leaving Arikara, it should also be noted that apparently only a very limited set of numerals are formed with the formative -waana, in contrast to Latin where the subtractive formation is also used for 28, 29, etc., at least through 88 and 89. So the issue of lack of productivity, noted at the end of §2.1, does arise here, even though in this case the formations seem transparent.

Greenberg mentions another language as providing exceptions similar to Arikara, namely “Montagnais, an Athabaskan language”, i.e., not the Algonquian language Montagnais or Innu, but the Athabaskan language Chipewyan or Dine Suline, earlier called Montagnais by French missionaries. Greenberg’s source is apparently Conant (1931: 53-54), which is listed in his References Cited and is itself based on Petitot (1876: lv). The examples in (16) show the forms given by Petitot (1876), in comparison with modern forms from Jaker (2014).

Most of the forms provided by Jaker are readily relatable to those from Petitot, though (16e) and (16h), if the forms in the two columns are indeed related, have undergone reduction in the current language that obscures their etymology.

Greenberg says that 9 is expressed as (10–1), that 8 is expressed as (4×2), and that 7 is expressed either as (10–3) or as (8–1), with the last being problematic for Generalization 14, since the system is overall decimal and does not use 8 as a base. The interpretation of (16g) seems straightforward, with ʔełk’é being a combination of the reciprocal prefix ʔełe- and the postposition k’é ‘on’, i.e., ‘on each other four’, i.e., 2×4=8; it parallels the expression for 6 (‘on each other three’). The interpretation of (16h) is also reasonably straightforward, with łá the stem for ‘one’; Petitot translates it more literally as “il y en a encore un en bas” (‘there is still one down’), referring to the fact that one finger has not been raised, i.e., 10–1=9 fingers have been raised. The same is true of (16e), for which Petitot gives the more literal translation “il y en a encore trois (doigts) repliés” (‘there are still three of them [fingers] bent’), so three fingers have not yet been raised, i.e., 10–3=7 fingers have been raised. Both (16e) and (16h) use the implicit minuend 10, as expected in a decimal system. The problem is (16f), which Greenberg interprets as 8–1=7. Petitot explains first how the speaker holds their hands to indicate 7: “Il unit quatre doigts de la main gauche, rapproche du pouce gauche isolé le pouce et l’index de la main droite’ (‘He joins the four fingers of the left hand, brings the thumb and index finger of the right hand towards the isolated left thumb’). He then explains the Chipewyan expression more literally as ‘on one side there are four of them’, which is also the English explanation given by Conant. While this may be a reasonable partial description of the configuration of the hands—there are four fingers joined together on one side—the expression seems to involve a fair amount of conventionalization (the left thumb is also extended, as are right thumb and index finger), and it does not lead to any interpretation along the lines of 8–1. This “exception” seems therefore to be spurious.

The third language discussed by Greenberg as an exception to Generalization 14 is Colonial Valley Zapotec (hereafter: CVZ), as described by Córdova (1578). For a fuller analysis of the system, see Sonnenschein et al. (Submitted); here I limit myself to those numbers that are relevant to Generalization 14, and to those numeral expressions that are relevant in the case of alternative expressions. CVZ has a vigesimal numeral system, although the linguistic expressions for the scores are often portmanteau, the intervening tens being expressed by adding 10 to the preceding score, as shown in (17), where the term for 30 is literally ‘twenty-and-ten’.

While there are different possibilities for expressing a number that is 15 above the next lower twenty (or equivalently, 5 below the next higher twenty), our interest will center on a formation that Greenberg identifies as subtractive, as in the version of 55 in (18).

This example clearly includes an element that means 5 and an element that means 60, so it not illogical to follow Greenberg in describing the construction as subtractive, i.e., 60–5=55. However, as with some of the other examples discussed in this section, the structure of the CVZ expression does not seem to be literally subtractive, although it can be subsumed under counting down as a subtype that Sonnenschein et al. (Submitted) call a “deficit” construction. The use of the definite prefix before a numeral, as in ce-caayo, is attested independently in the language and means ‘another x’ or ‘x more’, so a more literal translation of (18) would be ‘another five sixty’, i.e., if you had another five, then the number would be 60—but since there is a deficit of 5, the target number is actually 55. In other words, the literal interpretation of (18) is given by the equation in (19a), not that in (19b), even though both equations give the same result for x.

However, since I have suggested extending Greenberg’s Generalization 14 on subtraction to counting down constructions more generally, we can still ask the further question whether the minuend (in this extended sense) has to be a base of the numeral system in CVZ. Relevant examples are those between 15 above the next lower twenty and the next higher twenty, i.e., the range 16-19 above the next lower twenty, illustrated in (20) with the relevant CVZ expression for 56.

Greenberg interprets (20) as in (21a), which means that the minuend is 61, which is not only not a base of the system but also unlikely to be a salient number, given that the same pattern is found for 57-59, which would mean that 62, 63, 64 would also have to be salient numbers, which would deprive the notion of salience of any measurable import. Sonnenschein et al. (Submitted) argue that the correct interpretation of (20) is as in (21b), i.e., the value 56 is arrived at by first counting down 5 from 60 to get an intermediate result of 55, and then adding 1 to that intermediate result; the minuend would remain 60, a multiple of the base 20.

In effect, CVZ arrives at the value 56 by successive approximation, starting with 60, then counting down by 5 to give 55, then counting up by 1 to give the intended value of 56. A similar procedure is attested in Ket, as shown in (22) (Georg 2007: 181). In (21a), the value 80 is arrived at by subtracting 20 from 100; in (21b), the value 82 is arrived at by adding 2 to this interim result.

In other words, one has to know the rules that native speakers follow intuitively on how to “bracket” a complex numeral expression: in Ket, ((100–20)+2), and not (100–(20+2)), which latter would give the incorrect output 78. One might object that the bracketing proposed for CVZ examples like (20) does not follow the word division. However, it is unclear what exactly Córdova intended by the placement of orthographic word divisions, and much more likely that this had something to do with the language’s phonological structure than its grammar. The CVZ examples thus consistently show subtraction from a multiple of 20, followed where necessary by a process of addition to arrive at the final target value.

Greenberg (1978: 14) proposes a further universal on subtraction, which we can also extend to other instances of counting down:

Generalization 13: If a number n is expressed by subtraction as y–x, then every number z (y>z>n)⁹ is also expressed subtractively and with y as the minuend.

This generalization can be illustrated using the Latin examples in (14). Since 18 is expressed as (20–2), 19 must also be expressible by means of subtraction with 20 as the minuend, which is indeed the case since it expressed as (20–1). Greenberg notes that Chipewyan is an exception since 7 is expressed as (10–3) but 8 is not expressed as (10–2), even though 9 is expressed as (10–1). CVZ is also a counterexample on Greenberg’s analysis, since 56 is expressed as (61–5), but 57 is not expressed as (61–4), but rather, on Greenberg’s analysis, as (62–5). On the reanalysis proposed by Sonnenschein et al. (Submitted), the minuend is consistently 60 for numbers in the range 56-59 that use a combination of subtraction and addition, so this counterexample is removed. But going further, if 55 is expressed as (60–5), then according to Generalization 13 it should also be possible to express, for instance, 57 as (60–3), and so on. In fact, this is possible, since Córdova gives an alternative expression for 57 as in (23) (and likewise 56, 58, 59), which is clearly interpreted as ‘three more will walk to sixty’—the irrealis in CVZ can express future time reference— i.e., the interpretation is that there is a deficit of 3 with respect to 60.

So CVZ is not an exception. However, Ket, as illustrated in (22), is another exception, since although 80 can be expressed as (100–20) it is not possible, for instance, to express 81 as (100–19). The relevant factor seems to be that the subtrahend is rather large in relation to the minuend, which means that there is a large number of intervening numbers, some of which would themselves be quite complex. Indeed, this would violate another of Greenberg (1978: 13)’s generalizations.

Generalization 12: A subtrahend is always a simple lexical expression.

However, Ket does violate Generalization 12, as in (24), since the numerals 8 and 9 are themselves complex, being formed by means of subtraction: (10–2) and (10–1) respectively (Georg 2007: 180-181).

Clearly, we need to know more about subtraction before we will be in a position to reliably formulate meaningful universals of subtraction (and related counting down processes) that stand some chance of being valid. Part of the problem is the relative rarity of subtractive numeral formations, within which there is a preponderance of simple cases with a subtrahend of 1, sometimes joined by 2, while only larger subtrahends enable serious testing of the limits on the operation.

According to Greenberg, numeral systems in natural languages are always finite, i.e., for each natural language numeral system there is a highest number that can be expressed. This is formulated in Generalization 1:

Generalization 1: Every language has a numeral system of finite scope.

Note that it is clear that many languages have numeral systems of finite scope, and this is not at issue. Indeed, some languages have very restricted systems, such as Mangarayi with only 1, 2 and 3 (Merlan 1982: 92). Greenberg claims that the American English numeral system is finite, and his discussion suggests that this is true at least in his usage. But before addressing this important question, it will be necessary to discus a few preliminaries.

At issue are numeral expressions in the region that starts with the term million and its cognates in other languages. There are basically two different systems in operation, the short scale and the long scale, the latter with some internal variation, as shown in Table 1.

The short scale was, around the middle of the twentieth century, most associated with American English, but since then it has expanded to encompass most varieties of English, including in Britain. The long scale in used in most languages of continental Western and Central Europe, and was formerly prevalent in Britain. The intermediaries in -iard were not used in Britain, although at least some are used in continental Europe, with consistent use being found, for instance, in German. I return to some of these details below.

One relevant question is who actually uses or used the systems in question, in particular who made practical use of the systems, rather than just using the terms in academic discussion (as with linguists), i.e., methodologically actual usage is more reliable than intuition. Traditionally, such high numbers were the purview of astronomers, and it is no accident that such higher numbers are referred to as “astronomical”, though they are also encountered in some of the other natural sciences. The increasing size of national and international budgets from the mid-twentieth century means that higher numbers also came to be used regularly by economists. For languages spoken in countries that experienced hyperinflation, such as Germany in the 1920s, the practical use of such high numbers in economic contexts emerged earlier and even spread to the general populace. Studying linguistic practice under such circumstances can give us insight into how the numeral systems of languages are actually used.

But let us now return to the American English system as described by Greenberg, although some of the details have to be reconstructed from his discussion rather than being stated explicitly. My reconstruction of the relevant points is given in (25).

I emphasize that what is at issue is not whether the finite system as described by Greenberg exists, at least for some speakers of American English; I have no reason to doubt Greenberg’s characterization of his native-speaker intuitions. What is at issue is whether the finiteness limitation is a language universal.

I will now describe the numeral system, as it applies to higher numerals, as I internalized it in Britain in the mid-twentieth century. Lest it be thought that my account is purely academic and viewed through the imperfect lens of decades-old memory, I should point out, first, that as a child I read a lot about astronomy and so did encounter how British writers expressed large numbers, and second, that I was challenged to give an explicit description of this system by a skeptical linguistics instructor in the mid-1960s, which served to reinforce the system in my memory at a time when it was still in regular use. The relevant points are given in (26), with examples in (27); note that (a)-(c) are the crucial points, with (d)-(e) added for completeness.

Crucially, the system is recursive, since some terms, in particular trillion, can be repeated as many times as is necessary to express the relevant cumulative multiplication. Incidentally, in evaluating (26c), it is important to distinguish between the numeral and the homophonous noun. In English, this is easily done since the noun will stand in the plural if governed by a numeral greater than 1, while the numeral always remains in the singular. Trillion is thus a numeral in (28a), but a noun in (28b). (28d) is possible, since thousand is a noun, but not (28c), since numerals below million cannot be iterated. Note that the criteria for distinguishing numerals from nouns vary from language to language, so the tests valid for one language cannot simply be transposed to another.

The systems in (25) and (26) are very different from one another, even if there is overlap in some of the terms used (million, billion, trillion). The expression “two countries divided by a common language” seems particularly apt, even if in the intervening half century British usage has here moved in the direction of American.

One of the characteristics of Greenberg’s American English system as reconstructed in (25) is the strict application of the Packing Strategy, e.g., 10⁹ must be expressed as billion and cannot be expressed as thousand million; note that if the latter were possible, then 10³⁶ would be expressible as thousand decillion. Interestingly, there is one exception to the Packing strategy with lower numerals, presumably also for Greenberg (since it is generally widespread in American English), namely the possibility of expressing numbers in the thousands by counting in hundreds, i.e., (29b) and (29c) are both possible linguistic expressions for (29a), where (29c) violates the Packing Strategy.

However, searching on the Internet reveals that at least some speakers of American English do not share the strict constraints implied by Greenberg. Examples (30) and (31) are from the syndicated column of US astronomer Dennis Mammana (on whom further information is available on his web site http://www.dennismammana.com)¹², with (30) illustrating million trillion (where Greenberg would require quintillion) and (30) thousand trillion (where Greenberg would require quadrillion, in full three quadrillion five hundred trillion).

It is also useful to compare the situation in a selection of other languages, which is often very different from that in American English, certainly as described by Greenberg. French uses the long scale with intermediaries, but although terms from billion up are in principle available, in practice the highest monolexical term in general use is milliard, and higher numbers have to be expressed by using the components milliard and lower, as in (32), if necessary repeating milliard, as in (33). Both examples, incidentally, are from the prestigious newspaper Le Monde. Note that in French numerals from million up must stand in the plural (in -s) if preceded by a number higher than 1, and require the preposition de ‘of’ before a following numeral or noun, e.g., the relevant part of (32) is literally ‘the thousand milliards of dollars’.

German uses the long scale with intermediaries, indeed is often cited as the paradigm example of this type. However, while single lexical items above Billion are available, they tend to be avoided in practice; thus (34) avoids eine Billiarde ‘a billiard’, while (35) avoids eine Quadrillion ‘a quadrillion’. The numerals from Million ‘million’ up stand in the plural when governed by a number above 1, and are written with an upper-case initial, but unlike the corresponding nouns they do not allow an explicit linker to a following numeral or noun, e.g., (34) is literally ‘thousand billions friends’.

In German, I have encountered a number of examples where, contrary to principle (26e) in the characterization of the traditional British system (or at least my version of it), larger numbers precede smaller numbers in the set from Million up; an example is given in (37). Note that (26e) is not one of the constitutive principles of (26), which are (26a-c). This may indicate greater freedom in German here, though I would not be surprised to find individual variation in acceptability judgments in both languages.

Modern Arabic uses the European-origin terms milyōn, etc., following the short scale, though with bilyōn and milyār competing for 10⁹ (Ali 2013: 100-106). In Classical Arabic, however, the highest available numeral was ʔalf ‘thousand’, and “any number above 999,999 was referred to as 1000 multiplied by 1000 as many times as necessary” (Ali 2013: 108). Ali (2013: 108-109) gives textual examples, with (38) being the first part of a longer expression used by the tenth-century traveler, historian, and geographer Al-Mas’udi.

These examples should suffice to show that it is possible to combine high numbers, from ‘million’ in some European languages, from ‘thousand’ in Classical Arabic, in order to express a potentially unlimited range of higher number values. While (25) may be the correct characterization of the system used in (some varieties of) American English, it would be a mistake to extend its notion of an upper limit to all natural language numeral systems.

We may briefly consider one further generalization proposed by Greenberg (1978), namely Generalization 2.

Generalization 2: Every number n (0<n<L) can be expressed as part of the numerical system in any language.

In Greenberg’s notation, L is the number one above the upper limit of the numeral system, so what this says effectively is that every number from 1 up to the limit of the system is expressible within the system. In §3.1 I questioned the universal validity of L, so we can consider a slightly modified version of Generalization 2 that would say that there can be no gaps in a numeral system, i.e., if n is expressible in the system, then so are all numbers below n.

For Greenberg in 1978, the highest single lexical numeral in American English was decillion (10³³). In the meantime, higher monolexical numerals have come into circulation, e.g., centillion (10³⁰³). While speakers I have asked have generally accepted that there is such a word and that it would be the hundredth term in the series, they are often at a loss when I ask them to name the twentieth term in the series—though some do come up with vigintillion, which is also widely listed in dictionaries—and almost invariably at a loss when I ask them to name the twenty-third term in the series. While there are proposals on how to denominate such terms (e.g., the twenty-third would be tresvigintillion—see for instance https://en.wikipedia.org/wiki/Names_of_large_numbers), they have not caught on in usage, nor are most speakers aware of them. For speakers who have constraint (25a) in their system against repetition of higher numerals to express recursive multiplication, this means that there are some numbers between decillion and centillion that have no natural language expression, i.e., Generalization 2 is counterexemplified. At first it might seem strange that there should be such gaps in “counting”, but it should not be forgotten that no one in their right mind is actually going to try and count up to or beyond a decillion—if you were to count one numeral each second for a year with no breaks, you would only make it up to a paltry 31,556,952—so there seems to be nothing inherently wrong with a system where there are names for certain round numbers but not for certain numbers that occur between the round numbers.