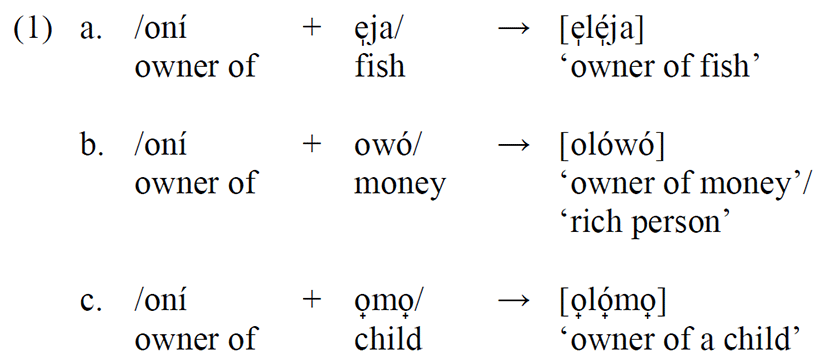1. Introduction
A numeral system is a writing system for expressing numbers. Numerals denote a class of specific group of words expressing quantity (Blažek 1999). They are definite/specific words in a natural language that represent numbers (Von Mengden 2010). Many researches have been carried out on the numeral systems by experts in linguistics (Abraham 1958, Oduyoye 1969, Sanusi 1995, Blažek 1999, Atóyèbí 2006, Wiese 2007, Fabunmi 2010, Oyebade 2013 among others). As observed in Wiese (2007: 760-761), number assignments, across languages, fall into three categories. One is the cardinality (i.e., the cardinal number assignments indicating the cardinality of a set) and they identify the numerical quantity of objects. The second is ordinality, which shows the position of an object within others, and the third type is the numbering system.
Therefore, the aim of this paper is to investigate the cardinal and the ordinal number assignments, the derivations as well as the mathematical operations involved in the Bàtɔ̀nū numeral system. The data used for our analysis in this study were drawn from Bàtɔ̀nū language spoken in the Baruten Local Government Area of Kwara State, Nigeria.
According to the researches carried out by Isa (1997: 1-10) and Sanusi (2002: 1), Bàtɔ̀nū is a language spoken as a mother tongue in a stretch of territory lying North-West and South-West across the Nigerian-Benin republic boundary. The language is specifically spoken as first language in former Western Borgu district of Kwara State, which now constitutes the newly created Baruten Local Government Area with its headquarters in Kosubosu. The districts that make up the new Local Government Area are: Okuta, Yashikira, Ilesha and Gwanara. In Benin Republic, the language is spoken in places like Parakou, Natintingou, Nikki, Kandi and other small towns and villages. Following Williamson & Blench (2000), Bàtɔ̀nū is classified under the Gur (Voltaic) subgroup of Niger-Congo, which is divided into two: Central Gur and Peripheral Gur. Bàtɔ̀nū is classified under the Peripheral Gur with some other languages like: Kulango, Win, Loron, Viemo, among others. Though the language is popularly known as Bàrùbá or Bàrìbá, the native speakers refer to it as Bàtɔ̀nū and refer to themselves as Bàt̀ɔ̀mbū. It is a tone2 language.
The following objectives have been set for the study:
i. To investigate the mathematical operations involved in the Bàtɔ̀nū numeral system.
ii. To apply a descriptive analysis using the lexical phonology and morphology approach in the derivational processes of the numeral system.
iii. To examine the agreement patterns within the different structural forms of the numerals.
iv. To examine the representation of number in quality and amount, in line with the system of forming complex numbers and counting operations.
To the best of our knowledge, Welmers (1952, 1973) are the major published research works on Bàtɔ̀nū, and the two works focused mainly on the aspects of phonology and morphology of the language. Moreover, some unpublished undergraduate and postgraduate research projects have also been carried out on various aspects of Bàtɔ̀nū language, namely Sanusi (1983, 2002), Togun (1982), and Isa (1997).
Welmers (1952, 1973), Sanusi (1983, 2002, 2003) are the previous works on Bàtɔ̀nū language that have examined the phenomenon of noun class system, the structure of the language, and the interdependency between the Bàtɔ̀nū morphological processes and phonological rules in word formation.
Sanusi (1995) discusses the Bàtɔ̀nū numerals that are directly related to the aspects examined in this study, in which he accounted for the traditional system of counting in base five and the derivation of compound numerals in Bàtɔ̀nū. In his treatment of numerals some aspects were not considered which informed the current effort. This study will therefore, carefully examine the Bàtɔ̀nū numeral system and expose its morphological as well as the mathematical operations used in the counting system of the language.
Various steps, theory and methods will be considered in the analysis and exemplification of the numeral system. It is hoped that this work will serve as a cornerstone for further studies on the numeral system in Bàtɔ̀nū and other natural languages; since the counting system is one of the universal features of human languages.
2. Theoretical Framework
Lexical Phonology (LP) and Lexical Morphology (LM) constitute the major framework adopted for our analysis in this study. Lexical phonology, according to Kenstowicz (1994: 20), receives generative interpretation of the relations between phonology and morphology. Our choice of the theory is therefore informed by its problem-solving efficiency. For instance, the lexical phonological theory, which exploits the interrelationship between morphology and phonology is capable of explaining phenomena in Africa languages (and indeed, numeral system in Bàtɔ̀nū), which are hitherto regarded as ‘complex’ or intractable.
The lexical morphology and phonology theory was developed by Mohanan (1982) and Kiparsky (1982a). This theory is based on the assumption that there are two types of phonological rule application:
• The lexical rules: this refers to rules that apply within the lexicon.
• Post-lexical rules: this refers to the output of two lexical components.
It is observed that rules that apply at the lexical level manifest different properties from those that apply post-lexically, but different properties will still be observed in the component.
This indicates that lexical phonology recognizes three levels of representations, namely, underlying, lexical and post-lexical. Below is a diagram of the overall structure of the lexical phonology model that serves as our theoretical framework in this study:

This representation shows that the word formation rules and the phonological rules can be divided into a series of levels or strata. Each level has the lexical phonological rules distinctive of that level.
Akinlabí & Oyebade (1987) apply this theory to vowel deletion in Yoruba, although the work leans heavily on Pulleyblank (1986), Halle (1973) and Mohanan (1985). Akinlabí & Oyebade rightly observe that the existence of phonological rules in Yoruba supports this proposal. This, according to them, occurs both lexically and post-lexically to attain vowel deletion as well as denasalization that transforms /n/ → /l/, as exemplified in (1) below:
The first process here is the deletion of vowel /i/ in “oní” and the second is the assimilation of /o/ to the initial vowel of the following morpheme. The third is denasalization which turns /n/ to /l/.
Goldsmith (1990: 20) also states that, “lexical phonology is arrived at by the concatenation of the morphophonemic rules and the purely phonological rules of the pre-generative years”. Hence, lexical phonology is proposed to account for the interrelationship between the two levels of linguistics, phonology and morphology.
In a similar way, we have applied the model to Bàtɔ̀nū data to attain similar derivational processes of deletion, assimilation and denasalization.
3. An Overview of Bàtɔ̀nū Numeral System
Bàtɔ̀nū operates a quinary (base 5) numeral system (Sanusi 1995). There are lexical items representing the numbers 1-5. Also, there are various possible combinations that exploit the cardinal numerical resources to build up an increasing system of counting by means of productive additive mechanism. This observation is aptly captured by Sanusi (1995: 14), that Bàtɔ̀nū uses base five or a multiply of five as the basis upon which both cardinal and ordinal numerals are derived. He also notes that “the numeral ‘six’ to ‘nine’ are derived based on five plus one through four, while ten is regarded as new unit (i.e., a multiple of five)”. However, similar to what Taiwo (2017) observes about ‘Prosodic Reduplication in Yorùbá’, Sanusi (1995) also sees the overall numerical system of Bàtɔ̀nū as a product of an interplay of morphological and phonological processes. The processes are employed to derive various numerical entities of different qualities and magnitudes. In Bàtɔ̀nū, they count from one (tía) to thousand (ǹᴐrubὺ/nᴐra). These counting structures are lexicalized in the language. The smallest unit of counting in Bàtɔ̀nūis ‘one’ and the counting system does go beyond thousand. Bàtɔ̀nū cardinal numerals are categorized into three broad groups as far as counting from one to thousand is concerned. These are the basic numeral, which is the most important aspect of the numeral system which all other numerals build upon. In clear terms, Omachonu (2013: 129) notes that “the basics are the primary numerals (simple cardinals) which are mono-morphemic in nature, while the derivatives are the secondary or non-basic numerals whose derivational history is traceable to a combination of the basic numerals through some addition or a combination of two bases”. We shall present and analyze the numerical systems in due course. We shall begin our discussion by identifying the basic simple and the derived simple cardinal numerals that constitute the figures in Bàtɔ̀nū language.
The lexical phonology model has become the focus of most generative research concerned with the relation of phonology to word structure. Kenstowicz (1994: 214) observes that lexical phonology develops the distinction between primary and secondary affixes into a well ordered morphology and the basic proposal is that Word Formation Rules (WFRs) and Phonological Rules (PRs) can be divided into a series of levels or strata. The LP model also defines a set of lexical items by a hierarchy of WFRS in which derivation proceeds through all the levels if no relevant morphology applies at that level and the output of each level is a lexical item. In deriving some numerals in Bàtɔ̀nū, two phonological rules are applied to the Underlying Representation (UR), these rules are the consonant deletion and vowel elision rules. The application of the two rules are exemplified in section 3.1.1.
The Bàtɔ̀nū cardinal numerals are categorized into three broad groups which are the basic, simple and the derived numerals. Basic numerals, according to Ajíbóyè (2013: 3), are those numerals that are not derived i.e., numerals whose form cannot be broken down into identifiable meaningful morphemes. Von Mengden (2010) considers the simple numerals as the easiest conceivable set of numerical expressions in a language which are mono-morphemic forms with arbitrary phonological shape. The basic and the simple cardinal numerals are lexically represented in Table 1 below. The first five cardinals are the basic numerals in Bàtɔ̀nū ‘base five’ counting system. They are used for counting and in describing quantity. The same kind of numerals are used for counting both human and non-human nouns.
Cardinal numerals 50 ‘fifty’, 70 ‘seventy’ and 90 ‘ninety’ in Bàtɔ̀nū are derived by adding ten (10) to each of the figures (i.e., 40+10, 60+10 and 80+10), etc., as exemplified in (2) below.
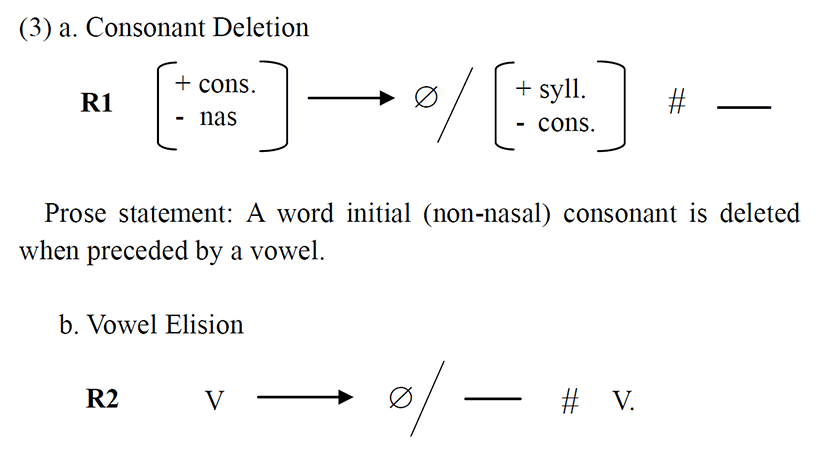
Bàtɔ̀nū uses five (‘5’) or multiple of five, as shown in table 1, as the base to which other numerals are added to derive numerals like: 6-9, 11-19 and 21-29. This derivational process is prone to phonological processes like consonant deletion and vowel elision. It is the initial consonant of the addition marker “kà” that is always deleted; while the vowel deletion involves the last vowel of the ‘number base’ five or any multiple of five that is involved in the derivation. Chumbow (1982) cited in Sanusi (1995: 16) postulates the following rules to account for the two phonological processes that take place before the derivation of other numerals. The rules are repeated here as (3) below:
Prose statement: The last vowel of a preceding word (i.e., a number base) is elided at the word boundary when it is contiguous with the initial vowel of the following word.
These two rules captured the derived numerals 6-9, 11-19 and 21-29. The first rule deletes the consonant of the coordinating element “kà” [k]; that is, the word-initial voiceless velar consonant [k] is deleted whenever it is preceded by a vowel. The second rule applies to the stem numeral “nᴐ̄ᴐ̄bù” signifying 5, “ↄkuru/wↄkuru” signifying 10 and “yendu/yenda” which stands for the figure 20. The final back high rounded vowel [u] of the basic unit is elided/replaced with the low back vowel [a]. Let’s consider the numerals in data (4) below:
A closer look at the data in (4) reveals the following. First and foremost, the entire numerical system is a function of compounding. However, this process generates certain phonological processes that include consonant deletion and vowel elision. This was reported by Sanusi (1995: 16) that “two phonological processes must apply before a correct output of a compound numeral is derived in the language”.
As observed in (4) above, since the voiceless velar stop [k] is deleted and the final back high rounded vowel [u] of the base is elided, we then derived “nᴐ̄ᴐ̄baìru” (‘seven’) instead of “nᴐ̄ᴐ̄buìru”, “ↄkuranᴐ̄ᴐ̄bú” (‘fifteen’) instead of “ↄkurunᴐ̄ᴐ̄bu” and, “yendaìru” (‘twenty-two’) instead of “yenduìru”. The deletion process further triggers vowel elision. Observation shows that the numeral ‘ten’ “ↄkuru/wↄkuru”, ‘twenty’ “yendu/yeeru”, ‘one hundred’ “wùnↄbù/wùna” and ‘a thousand’ “nɔ̀rubù/nᴐra” are in free variation (can substitute for one another with no subsequent change in the word meaning).
The above examples in (4) show that the rules are in the feeding order (i.e., if one does not apply, the other cannot apply). Observation shows that the rules of deletion and vowel elision proposed by Chumbow (1982) do not apply to numerals from thirty and above. Sanusi (1995: 19) also notes that (R1) is independently motivated in the language whenever the use of addition marker is required to derive a compound numeral. However, an informant hinted that when counting from thirty-five and above, the application of rule one becomes optional, hence the addition marker within a derivation could be realized as an autonomous word.
Sanusi (1995: 16) states that ordinal numerals are used to indicate the exact position where something occurs in a series. He opines that “apart from the first ordinal numeral, other ordinal numerals in Bat̀ↄnu are formed by adding the positional suffix morpheme “-sèé” which represents the English equivalent of ‘-nd’ as in 2nd, ‘-rd’ as in 3rd, and ‘-th’ as in 4th to each of the cardinal numerals”. In Bàtɔ̀nū, there is a separate and distinct expression for ‘first’ which is derivationally independent of the cardinal ‘one’. Observation shows that there is no synchronic or diachronic morphological connection between “tía” (‘one’) and “gbiìka/gbiíko” (‘first’). All the ordinal numerals in Bàtɔ̀nū paradigm are regularly derived from the cardinal numerals via suffixation “-sèé” except for “gbiìka” (‘first’) which is derivationally independent of other pairs. It behaves morphologically exactly like the other numerals while other paradigm is absolutely regular and free of suppletion. This could be exemplified in Table 2 below:
Table 2 above shows that there is no synchronic or diachronic morphological connection between “tía” (‘one’) and “gbiìka” (‘first’). Also, Table 2 shows that there are only two independent ordinal numbers found in the lexicon of the language, that are not derived. They include “gbiìka” (‘first’) and “dàkùrè” meaning ‘last’. The others are formed by the addition of the ordinal indicator “-sèé” to the cardinal number base.
The mathematical operation involved in the derivation of some numerals in Bàtɔ̀nū is ‘addition’. Sanusi (1995: 16) asserts that “an addition marker “kà” meaning ‘add’ in Bàtɔ̀nū is used as an arithmetic operator to add any number to the number base”. Therefore, the number unit ‘one’ to ‘five’ are added to “tèna” (‘thirty’), “weèru” (‘fourty’), “weèraↄkúru” (‘fifty’), “wàta” (‘sixty’), “wàtakàↄkúru” (‘seventy’), “wène” (‘eighty’), “wènekàↄkúru” (‘ninety’) to derive compound numbers. The process of addition is expressed with the additive morpheme “kà” (‘add’) to connect the appropriate unit to a particular base to derive intended number.
The derivational strategy employed to derive 30 upward is structured in such a way that the additive ‘kà’ does not undergo neither consonant deletion nor vowel assimilation. Consider the examples in (5) below.
Nigerian currency is called “Naira” and its denominations are: “Naira” and “Kobo” (₦: K). Officially, the currency notes are embossed with the pictures of distinguished Nigerians. Among Nigerians, each currency note is called by the name of the personality on the currency note. For example, twenty naira note (₦20) has the picture of the Former Military Head of State (late Gen. Murtala Muhammed).
It should be noted that of all the personalities appearing on the currency notes, late Murtala Muhammed happened to be the most popular, as people refer to the twenty-naira (₦20 note) that bears his photograph as “Muri” (the abbreviated form of Murtala) especially among the Yoruba people (see the appendix). This practice is also replicated in the Bàtɔ̀nū counting system in which the abbreviated name “Murí” is borrowed from Yoruba (the neighboring language).
However, money is counted in Bàtɔ̀nū with the name of the currency coming before the numbers e.g., “ḱↄb̀ↄ”, “nérà”. Bàtɔ̀nū borrowed the concept “Múrí” (i.e., twenty) coming before the numbers e.g., Múrí tía (twenty in one place), Múrí ìru (twenty in two places), Múrí ìta (twenty in three places). Counting of money in the language also employs the use of the term “b̀ↄru” literarily ‘a bag’ in which a bag represents two hundred (200) Naira. In other words, multiples of 200 are counted in bags. For example, “nérà bɔ̀ru-tía” ‘one bag of Naira’ (N200), “nérà bɔ̀ru-iru” ‘two bags of Naira’ (N400), “nérà bɔ̀ru-ita” ‘three bags of Naira’ (N600), etc. They also count in thousand, and multiply “nérà nↄrↄbu” ‘a thousand Naira’ with any caidina number.
Counting of money through addition is achieved by the use of “kà” (a conjunction) in order to derive larger unit. Sanusi (1995) asserts that addition marker “kà” meaning ‘and’ in Bàtɔ̀nū is used as an arithmetic operator to add any number to the number base. Also Alerechi & Igbo (2013: 316) opine that one of the complexities in the numeral system is the number derivation which involves the use of combined words/numerals through some mathematical processes which include: addition, subtraction, multiplication and combination of different mathematical processes to yield certain numerals. The examples in Table 3 below show how the addition mechanism operates in Bàtɔ̀nū money counting system.
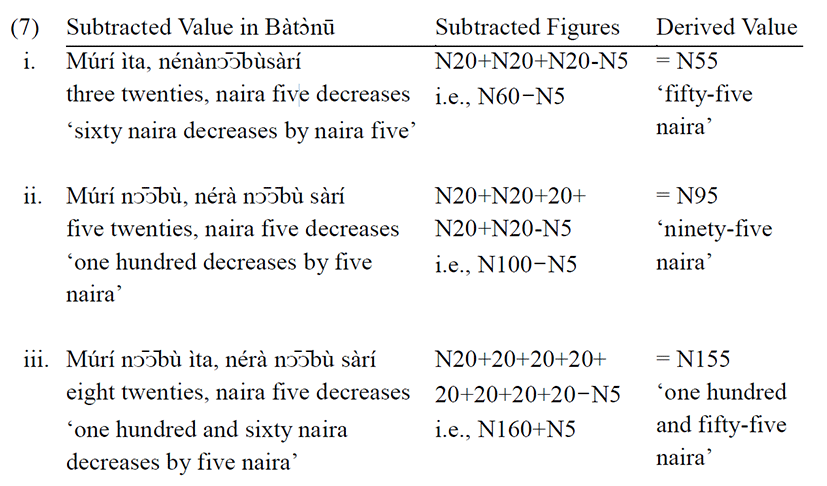
Subtraction can occur in isolation to derive numbers, and in combination with other mathematical operations. Sanusi (1995: 17) observes that in some cases where the language considers a process of addition to be cumbersome, it uses the subtraction method as an alternative approach in which the language considers the process of subtraction to be much easier than the process of addition. Here, the suffix morpheme “-sàrí” is affixed to the money counting base (i.e., positioned after the number from which a number is subtracted), which is conventionally coded as ‘decrease/less/reduced’. The process of subtraction is involved in generating multiples of twenty and hundred. The subtractive morpheme “-sàrí” is positioned at the end of the numerals and changing its position can violate a correct derivation. The examples in (7) show the internal structure of counting through subtractive method.
From data (7) above, it could be observed that N20 is no longer expressed as “néràyenda” which is equivalent to twenty naira but as “Múrí” (in twenties). However, an omission of the operative unit “-sàrí” or a violation of the order of occurrence of the items will cause the derivational process to ‘crash’. This twenty Naira (N20) note bears the picture of the former military Head of State (late Gen. Murtala Muhammed).
Olúbòdé (2013: 193) notes that in multiplication, the counting system has multiplicands and multipliers. The multiplicands are the numbers that are to be multiplied by another while the multipliers are the sequences of multiplications. Olúbòdé (2013) shows that multiplication is used in generating decades, hundreds and thousands, by giving examples in Yoruba saying “multiplicands are base numbers such as ‘Ogún’ (20), ‘Igba’ (200), and derived bases such as ‘çgbàá’ (2,000) and ‘çgbàáwàá’ (20,000)”. In Batↄnu the multiplication method is achieved by multiplying a simple and derived cardinal numerals by “bɔ̀ru” ‘a bag’ (denoting two hundred Naira) for counting from 1,000 - 5,000. “Bɔ̀ru-” is prefix to the other numeral which indicates a multiplication of that numeral with ‘a bag’ (200). If “bɔ̀ru-ìta” is 200 x 3 the multiplicand will be 200 and the multiplier is 3. In this case, the multiplier still goes on to 9, after which another base “nɔ̀rↄbù” (thousand) is reached. “nɔ̀rↄbù” here is also a multiplicand which is constant, the multiplicands are in the first position and its multiplier occupies the last position. Moreover, multiplication process involves the sequence of the higher and lower units without an intervening morpheme, because the sequences of numerals denoting multiplicative process are left bare. This can be exemplified in Table 4 below:
As shown in Table 4 above, when the amount involved is up to a hundred, “bɔ̀ru” (‘a bag’) is used to measure the amount, so N200 ‘two hundred naira’ is referred to as “bɔ̀ru” in Bàtɔ̀nū language and half a bag is called “bɔ̀nu”. Thus, instead of counting N300 (three hundred Naira) as “bɔ̀rukàmúrínᴐ̄ᴐ̄bù”, it is counted as “bɔ̀rukàb̀ↄnu” literarily ‘two hundred and a half bag’ since half of two hundred Naira (N200) is one hundred Naira (N100).
In the course of this research, we discovered that Bàtɔ̀nū borrowed the term “naira”. The Batↄnised forms of ‘naira’ and ‘kobo’ are “nérà” and “ḱↄb̀ↄ” respectively, while the concept “Múrí” is borrowed from Yoruba (which is a neighbouring language). Up to the present time, counting of money still follows the system as shown in (7) on page 76, and it differs slightly from the ordinary counting system, due to the prefix attached to the number base.
4. Major Findings
This study has examined the mathematical operations involved in the Bàtɔ̀nū numeral system and the major findings of the paper include:
i. We discovered that individual word presents individual number base, such as wɔkuru/ɔkura ‘ten’ (10), yendu/yeeru (20), wùnᴐbù/wùna ‘one hundred’ (100) and ǹↄrubù/nↄra (1000). Others are: gbiìka/gbiìko ‘first’, non-ìru/non-meru ‘twice’ and tía/teeru/turo ‘once’.
ii. Except for ‘first’, all ordinal numerals are derived from cardinal numerals with the addition of a suffix morpheme “-sèé”.
iii. Each of the simple cardinals: “nᴐ̄ᴐ̄bù” (‘five’), “ↄkuru” (‘ten’) and “yendu” (‘twenty’) changes its form and becomes “nᴐ̄ᴐ̄ba”, “ↄkura” and “yenda” respectively, whenever it co-occurs with another numeral to derive a new number.
iv. For the sake of simplicity, Bàtɔ̀nū employs subtractive mechanism in the derivation of numerals. The language uses productively the additive marker “kà” meaning ‘and’ in adding other base numerals. Generally speaking, it could be observed that money counting system in Bàtɔ̀nū employs the mathematical operations of addition, subtraction and multiplication in order to simplify the counting system.
5. Conclusion and Recommendation
As indicated earlier, the primary aim of this study is to give a vivid description of the Bàtɔ̀nū numeral system, and of course show the mathematical operations involved in the derivation of the numerals. In carrying out this task, effort was made to use insights from the theories of phonology and morphology to explain the processes involved in the numeral formation.
Though this report may not be exhaustive, it is hoped that the study has achieved its primary aim of providing a detailed description of the morphological derivational processes in Bàtɔ̀nū numeral system. It has been demonstrated that Bàtɔ̀nū numerals can be derived or non-derived. It has also shown that its subtraction device, in money counting system, is overtly reflected in the word “-sàrí” (‘decrease/reduce’).
Finally, it could be said that the Bàtɔ̀nū system is rich in expressing numerals for its cultural and scientific needs, without any cause for borrowing from another language, except for the symbols used in counting money, which are refashioned by the Bàtɔ̀nū native speakers in order to suit their purpose. For example, the notions ‘Naira’ and ‘Kobo’ are refashioned as “nérà” and “ḱↄb̀ↄ”.
We have thus far explored and analyzed the structure of Bàtɔ̀nū numeral system. There are, however, residual issues that require further research. This includes, among others, a detailed morphosyntactic description that captures the various distributions of these numerals in different linguistic and cultural domains.
Finally, it is hoped that subsequent or further research into the numeral system of Bàtɔ̀nū will include discussions on much more comprehensive descriptive grammar of the Bàtɔ̀nū numeral system and other related issues including reference to time expressed in hours, measurement, and the dating system.