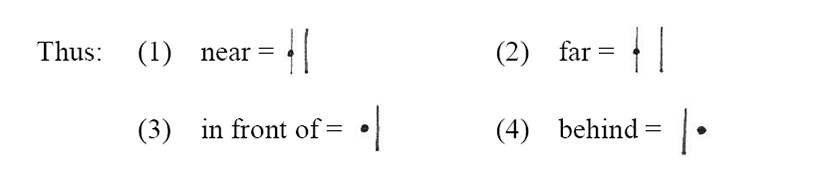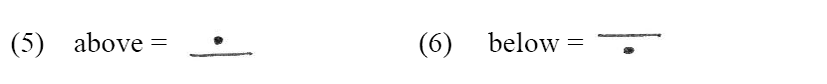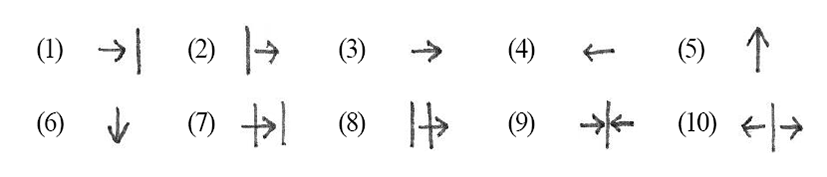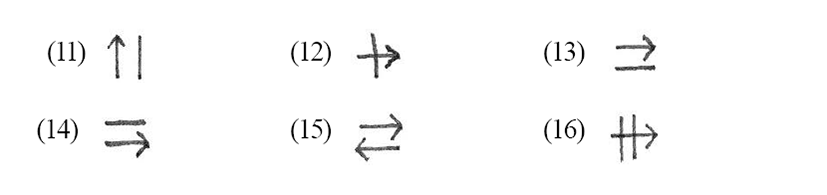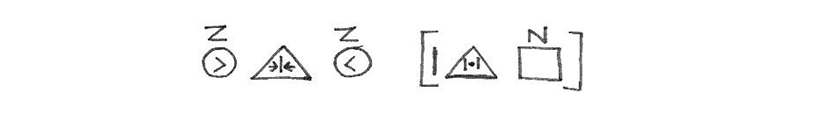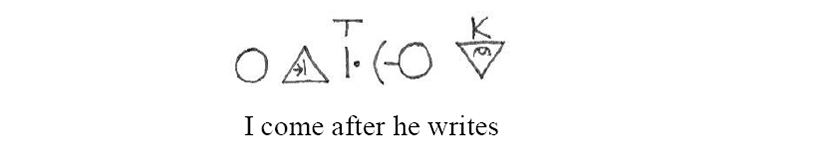Karl Haag, Modern Linguistics, and ‘Real Character’

1. Karl Haag: Life

Although almost entirely unknown or forgotten today, the German dialectologist Karl Haag (1860-1946) was, in his time, an eminent contributor to the field of area linguistics, as well as writing papers on the general structure of language. Born in Schwenningen am Neckar (modern-day Villingen-Schwenningen), Haag was a native speaker of the local Allemanic-Franconian dialect, and it was this that gave him an interest in dialects and language in general. In his youth he studied a number of foreign languages and could read Latin, English, French, Italian, Spanish, Dutch, and Swedish. As a teacher in a Gymnasium [grammar school] he was able to use his summer holidays to go walking and research the dialects of Germany. He also travelled in Turkey and North Africa. With such a wide variety of foreign languages at his finger-tips, he was able to turn his mind to a theory of the general structure of language and to ways of representing its logical structure. He wrote continually between 1888 and 1946 on dialectology and linguistic theory. He died in 1946 at the age of 86 in the town of Künzelsau in Baden-Württemburg, southern Germany (Benzing 1951).

Towards a Logically-based Graphic Language [1902]

Towards a Logically-based Graphic Language [Versuch einer graphischen Sprache auf logischer Grundlage, hereafter referred to as Versuch] appeared in 1902, surprisingly early in the career of a linguist, given that its aim is no less than an attempt to reveal the very basis that underlies not just the structure of German, but the structure of language in general. Published by Kohlhammer in Stuttgart, it is a slim booklet of 83 pages, written in a dense, very technical, and very individualistic style. Kohlhammer have no record today of the print-run but believe it to have been very small (Personal communication, Christina Jabs, Kohlhammer Verlag, June 2016). On the cover, his name appears as ‘Carl Haag’ but the usual spelling of his first name is ‘Karl’.

Haag had developed a symbolic language to demonstrate his theories, but the practicalities of printing meant that it was impossible to incorporate his hand-drawn symbolic examples into the text, and they had to be appended in a separate section at the end. This certainly causes difficulties for the reader, not only because he or she has to turn constantly from text to appendix while reading, but also because there is no exact match between the examples given in the text and their position in the appendix.

The book is long out of print and together with other works of Haag must be sought in libraries, on the Internet or on the premises of antiquarian booksellers. It has never been translated into English. Moreover, it does not figure in the large-scale reviews of universal and artificial languages such as Couturat & Leau (1903), Pei (1951), Large (1985), Yaguello (1991), or Okrent (2009). It is perhaps for these reasons that the work has been all but forgotten, although, paradoxically, it has an important place in the history of artificial and universal languages, as I shall attempt to demonstrate in the following pages.

Even though it is contained in a mere 70 pages of text and 13 pages of symbols and diagrams, Haag’s system is immensely complex. Any explanation of it must proceed by degrees, as each of Haag’s approaches to aspects of language is closely tied to each of the others, and a careful unravelling must be undertaken if the reader is ultimately to be able to see how the system interlocks and functions. I must therefore crave a degree of patience and indulgence on the part of that reader as I attempt to recreate Haag’s system in an intelligible and practical format. Thereafter follows a critique of the work, and links are made to contemporary work in linguistics and to work on a modern ‘Real Character’ (see Maun 2013, 2015).

3. Historical Context

Haag’s work took place at the confluence of two streams of historical and contemporary influence.

The first was that of ‘universal language’. The history of artificial languages and Real Character has been briefly outlined in two previous papers in this Journal (Maun 2013, 2015). Since the seventeenth century, there have been many attempts to find a way of representing language such that anyone, whatever his or her native language, can understand a message passed between two people. Leibniz hoped to produce such a system and referred constantly to it in his writings (Eco 1985, Davis 2000, Maat 2004), going so far as to believe that an ‘algebra of thought’ was possible, a representation of language that would enable people to discover the truth or falsehood of a statement merely by calculating, using symbolic figures. Needless to say, his efforts ended in failure. Other systems such as those of Cave Beck (1657), a schoolmaster, used numbers to represent words, set against an alphabetic list in English. The need to understand English before one could use this allegedly ‘universal’ system seems to have eluded the author.

The two great ‘universal’ systems of the seventeenth century were those of George Dalgarno (1661) and Bishop John Wilkins (1668). Each attempted to divide the world into a number of classes and thereafter represent the members of those classes by symbols. Verses containing the vocabulary, or long complicated tables acted as route-maps to enable readers to find the words that they sought. The system of symbols devised by Wilkins (‘the Real Character’) also had a spoken version (‘the Philosophical Language’) in which letters combined to form pronounceable words.

In the eighteenth century, de Maimieux’s Pasigraphie [i.e., pasigraphy, a language meant only to be read] (1797) resembled in some aspects the table-based system of Wilkins. It used a system of twelve combinable symbols and the length of a ‘word’ formed from their combination would in part define to what category of reality the word referred, while a set of tables served as points of reference. The system enjoyed some success for a while.

Such schemes, however, were destined to be eclipsed by ‘the artificial language movement’. In essence, the artificial languages produced in the 19th and 20th centuries either used grammatical classes which were filled with arbitrarily-formed and combinable syllables to make words, e.g., Ruggles (1829) and Edmonds (1856), or took elements from existing languages (e.g., roots, prefixes, and suffixes). These elements were put together to create a new language, e.g., Esperanto (Zamenhof 1887), the best known of these creations.

Needless to say, it was the latter type, such as Volapük (Schleyer 1880), Interlingua (Peano 1903), Ido [1907] (de Beaufront 1919), Occidental (de Wahl 1922) and Interglossa (Hogben 1943) which were more successful (in a limited way) and easier to learn than the creations of Ruggles and Edmonds, but only if one was a European, as they all used the major languages of Europe as their basis. A speaker of an Algonquian or Bantu language would certainly have struggled to see the logic of such languages and would have found little to grasp in the system of word-formation. Nevertheless, such was the power and momentum of the movement towards artificial languages at the time, that, in 1903, Louis Couturat and Léopold Leau produced the massive Histoire de la langue universelle, an essential reference work on the subject, even today (Couturat & Leau 1903). (More recent broad studies of the artificial language phenomenon include those mentioned in my introduction to Haag’s work, above.)

Even at the time of Couturat and Leau, however, the idea of an international auxiliary language was changing. This is exemplified by the work of Carus (1904) whose ‘Suggestions for a Pasigraphy’ outlined a visual vocabulary and a syntax based on place-value, rather like a musical stave, an idea which went back to the work of Francis Lodwick published in 1666 (Salmon 1972).

The second set of influences on Haag was more contemporary and came not from the field of linguistics but from mathematics and logic.

Since the time of George Boole (b.1815), there had been a gradual trend towards bringing logic and mathematics together. In 1879, the German logician and mathematician Gottlob Frege (b. 1848) had published Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens [Conceptual script, a formula language of pure thought modelled on that of arithmetic] (Frege 1879). Frege’s principal goal was to demonstrate that arithmetic could be reduced to logic. In the Leibnizian tradition, he recognised that to do so he would require an appropriate symbolism, just as arithmetical, geometrical, and chemical symbols allowed interpretation and calculation within their particular fields. The reduction of mathematical expressions and equations to logical propositions could be achieved by the use of letters for numbers and the introduction of symbols for arithmetical functions and logical operators (and, or, not, etc.).

He notes in his preface to Begriffsschrift, ‘If it is a task of philosophy to break the power of words over the human mind, by uncovering illusions that through the use of language often almost unavoidably arise concerning the relations of concepts, by freeing thought from the taint of ordinary linguistic means of expression, then my Begriffsschrift, further developed for these purposes, can become a useful tool for philosophers’ (pp.50-51). It should be noted that the Begriffsschrift is purely a pasigraphy, a language written to be read. There is no spoken version and it cannot be read aloud, other than by interpretation.

Not only did Frege reduce mathematical propositions to symbols, he also brought out logical structure through the use of an early type of tree-structure (similar to those later used by transformational grammarians) which showed how premises and conclusions were linked to together. Pure thought was thus given visual expression, but this did not represent a map of the mind. Such pure thought was expressed in the world through the script and truth functions could be calculated from the representation thus given.

As Legris (2012: 95) notes, ‘[I]t can be argued that the formal script was also conceived to represent formal structures. This representational side has […] the following main features: (i) there is only one structure (the world) to be directly represented, (ii) it is an ontological representation: it represents basic components of reality. As a result, the tension … between calculus and representation can be found also in the case of Frege’s script. This has been expressed traditionally by saying that Frege’s conceptual script is conceived as a universal language.’ Frege’s was not, of course, a description of natural language, but a limited and formalised system which went some way towards the ideal symbolic language of Leibniz.

Haag’s work, then, was carried out just at the time that universal language and logical representation occupied the thoughts of both intellectuals and idealists. The 1900 Paris conference on the possibility of an agreed International Auxiliary Language brought together both Esperantists, e.g., Couturat, and mathematical logicians, e.g., Russell and Peano. Haag’s little book of 1902 was yet to surface with its new ideas. Haag’s own work was in some ways influenced by both streams of thought but his own approach was to be both individual and innovative.

4. Haag’s Critique of Artificial Languages

Versuch opens with a damning critique of artificial languages of the Esperanto type:

Haag thus has no desire to create a language of the type described by Couturat & Leau as a posteriori. In the view of these two authors, what characterises a posteriori languages, such as Myrana (Stempfl 1889) or Universala (Heintzeler 1893), is the eclectic internationality of the vocabulary base and the grammar. It is this ‘plundered detritus’ which, in Haag’s view, is the principal weakness of the contemporary artificial languages, as logical structure is thereby destroyed. Such languages are thus neither a priori (created through an initial logical analysis of the world and bearing no resemblance to natural languages) nor mixed (created by combinations of elements drawn from natural languages, but insisting on invariable logical rules, much like a priori languages.).

Haag’s aim is different and its stands out in a peculiarly significant way:

Haag does not wish to create a new language which can be used, but to demonstrate the underlying logical structure of all language in a visual fashion.

The presuppositions inherent in Haag’s belief in ‘conceptual content common to all languages’ and the possibility of its being ‘free-standing and independent’ will be discussed below in Section 14.

5. Terminology

Haag is concerned to show how language, and therefore thought, demonstrates its own logical structure. At the centre of his analysis lies the proposition or judgement (Urteil), the foundation stone of classical and medieval logic. From the time of Plato and Aristotle, logicians have concentrated on the truth or falsehood of statements and the logical means by which such values may be determined. Haag, however, shows little concern with such syllogistic demonstrations. His aim is to show that initial statements are tightly structured and to demonstrate how such structure may be shown in a symbolic, logical, but language-neutral way.

Haag’s basic analysis of a sentence is similar to the traditional grammatical analysis into subject (a person, thing, or topic about which something is said) and predicate (that which is said about the subject). In grammatical terms, of course, the predicate is everything in the sentence except the subject. Haag is more focused, however, and chooses a system which is more close to logic, that is, an argument-predicate structure, where argument is roughly equivalent to noun and predicate is roughly equivalent to verb or adjective. James Cooke Brown, the designer of Loglan (1975: 85) summarises such a structure: ‘Predicates make claims. Arguments designate the individuals, or sets of individuals, those claims are about.’ Thus, both The cat is large and The large cat show argument-predicate structure, although of different kinds. Both are equivalent to: There is some A such that, if A is a cat, then A is large.

This double form of predicate structure is reflected in Haag’s curious choice of vocabulary for his two logical sentence-elements, Träger and Verhalten. The former literally means carrier (from tragen, ‘to carry’ or ‘to bear’) and the latter, behaviour. These terms make both the understanding and an English translation of Haag’s text extremely difficult. The terms Argument and Prädikat already existed in logic in German but Haag chose not to use these. Nor did he choose Frege’s German terms Argument and Function [sic]. The author’s choice of terms which differ from these shows (a) that he was not beholden to any existing system of logic or contemporary approach to logico-mathematics, and (b) that he was trying to convey something slightly different. Indeed, there is no mention or acknowledgment in Versuch of the influence of any other writer, least of all Frege.

Haag’s notion of Träger corresponds in the main to that of the noun or noun phrase that fulfils the grammatical functions of Subject and Object (direct or indirect) in the sentence. A Träger is both a carrier of meaning (its referent) and of function, much like a tagmeme in the system of tagmemic analysis developed by Cook (1969) and Pike (1982). A tagmeme (unit) is both a grammatical slot and its filler, e.g., in The cat is large, The cat is a tagmeme having the reference [CAT] and filling the grammatical slot [SUBJECT]. In Haag’s system, the subject of the sentence is known as the unabhängiger Träger (independent Argument) and both direct and indirect objects are abhängige Träger (dependent Arguments).

Verhalten is more complicated. As noted, its central meaning is behaviour, but in Haag’s use the term covers both verbs and adjectives, i.e., it covers both action and attributes. It is also clear that Verhalten, in Haag’s idiosyncratic usage, bears a resemblance to Verhältnis, meaning relationship, i.e., the relationship of a verb or an adjective to a noun by virtue of an action depicted, or the attributes, qualities, or properties ascribed to the noun.

Haag is far more concerned with Verhalten than with Träger. Unlike the ‘language projectors’ of the 17th and 18th centuries (Wilkins, Dalgarno, de Maimieux, etc.), his aim is not to draw up a catalogue of things contained in the world, neatly classified into tables and columns, i.e., an a priori language. Rather, he aims to show in particular how mental concepts derived from bodily experience (e.g., near, far, above, below) can form the basis of a system of predication in which these concepts extend beyond their initial spatial field into the domains of mechanics, biology, and psychology. His neglect of Arguments, in particular, nouns, will be examined below in Section 14.

This concern with Verhalten reaches a degree of complexity when Haag takes a concept such as inside and notes that, depending on its context:

Depending on its usage, then, a Verhalten can become a Träger (inside becomes to go inside, to penetrate, and ultimately the thing which goes inside, i.e., a claw or a thorn). Later semanticists such as Leech (1974) use the term predication downgrading for the process whereby a Verhalten (in Haag’s terminology) becomes a Träger, e.g., A person (Argument) who rides a bicycle (Predicate) becomes A bicycle-rider (Argument).

While no set of English logical terms corresponds exactly to Haag’s use, I shall here use the terms Argument and Function, following Frege’s usage, rather than that of the later Leech. This provides terminology which is contemporary with Haag and avoids any possible confusion between logical predicate (e.g., verb or adjective) and grammatical predicate (everything in a sentence which is not its subject). Furthermore, I shall retain the upper-case initial letter of the German to differentiate Haag’s use of Argument and Function from the everyday use of the words argument and function. It must, however, be borne in mind that Haag’s use of Function is very fluid, allowing changes in concept or category.

6. The Basis of Haag’s Conceptual System

Haag begins not by looking at language, but by looking at the human being and human perceptions. Language, he believes, derives from the fact that humans are embodied beings in a world which they perceive through their senses, and it is these senses and the perceptions which they provide that are the basis of thought and speech. The spatial is thus the central concept in Haag’s system. Concepts such as ‘time’ will later be derived from the central notion of ‘space’.

The four most important perceptions of space for the human being are the horizontal and the vertical, the distant and the enclosed, and relationships between objects are seen as obtaining in these fields. The first of these relationships are on the distance axis, namely near and far. Thus, A is near to B or A is far from B. From these may be derived in front of and behind, on the horizontal axis, orientation and visibility influencing the choice of term.

It should be noted here that Haag is primarily concerned with Functions, not with Arguments, i.e., he looks at the relationships of A to B, C to D, E to F, e.g., A is near to B, C is far from D and E is in front of F, etc. (as we have briefly seen in Section 5). However, these Functions can become Arguments, i.e., the symbols for proximity, distance, and precedence (nouns) will be based on the underlying spatial concepts and their symbols.

Haag expresses relationships such as the above symbolically:

Download Original Figure

On the vertical axis come above and below: A is above B or A is below B.

Download Original Figure

Two other spatial perceptions are important (1) whether something is inside or outside another thing (2) whether something is open or closed. Haag thus arrives at the last four of his principal notions:

Download Original Figure

7. Force Levels

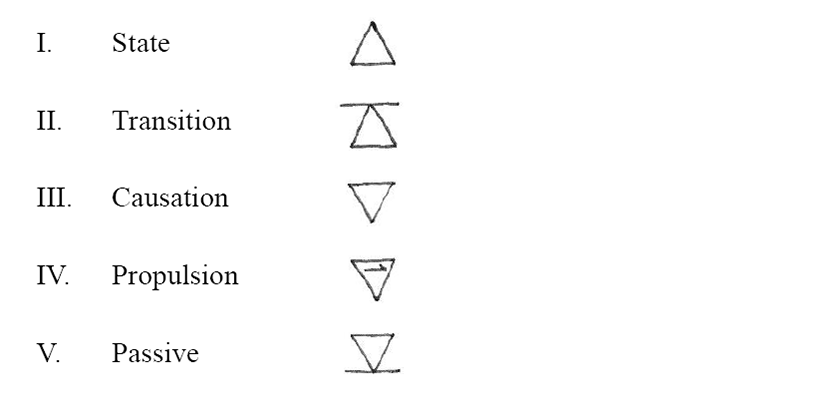
Before considering Haag’s other central concepts and their symbolic representations, it is necessary to introduce his notion of Dynamic Conceptual Levels or Force Levels, of which there are four, with a fifth expressing the passive sense.

Haag’s principal concepts (and many others) may be used at several levels, though not necessarily at all levels. They may described, using Haag’s Roman numerical notation, as follows:

Haag defines the differences between these Levels. Figures in square brackets have been inserted for clarity:

As an example, Haag writes:

Level IV (Propulsion) for inside would mean to force in, to drive in and Level V (Passive) would mean to be occupied.

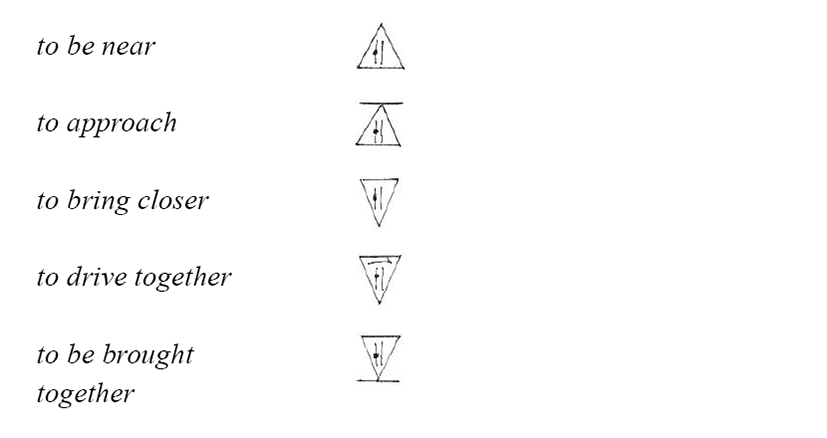
The first four of his concepts (near, far, in front of, and behind), used as Functions, would thus have the following meanings, according to the force level at which they were used:

To show at which Level a concept is being used, Haag uses triangular borders around its symbol. The levels are symbolised thus:

Download Original Figure

For the concept near, the combination of prime and border gives:

Download Original Figure

8. Additional Spatial Primes

On the basis of the first ten spatial primes (above), Haag creates a further ten which operate at Level II, i.e., Transition. Each is based on motion, relates to a source or goal, and corresponds to a prime at Level I (given in brackets in the following examples). Thus, at Level II:

These are symbolized as follows.

Download Original Figure

A further six spatial primes relate to what might be described as a ‘transitory’ relationship with another person or thing. Haag notes:

These six concepts are:

They are symbolised as follows.

Download Original Figure

9. Degree

The twenty-six primes (10 at Level I and 16 at Level II) provide the foundation-stone on which the remainder of Haag’s system is based. He later provides further symbols for more precise spatial concepts such as directly in front of, immediately below, etc., but we need not concern ourselves with these here.

More important than these additional space-related terms are those of Degree which can modify a term or express a relationship between two arguments involving measurement, negativity, or definition.

Haag then justifies his use of mathematical symbols to represent these concepts (although he lists them in reverse order in his examples as shown below):

Haag’s 11 symbols of degree, as shown in the original visual order are shown below in Table 2:

These concepts of Degree may be added to members of the spatial category and to others described below. Thus for the category of Space, the following emerge from the application of Degree:

10. Expanding the Categories: Fields and Senses

Haag now goes on to expand his basic cognitive notions into other fields, thereby expanding the possibilities both for predication (Functions) and entities in the world or the mind (Arguments). Rather than create arbitrary or even motivated symbols for each category, he chooses to use the initial letter of a Greek or Latin word which corresponds to his German nomenclature. Note: The original Latin or Greek has been deduced from Haag’s initials.

It is now possible to apply Haag’s concepts of Degree in these other fields. By way of example, the degree concepts 17-20, used in Table 3 in a spatial context, now produce the following meanings when used in other fields:

Note that for the most part these applications produce predications, i.e., Functions, but in the Typological application, an Argument may be produced, namely ‘feature’.

To the 26 spatial concepts and the 11 concepts of degree, Haag now adds 10 which derive from the senses:

These are as follows:

Symbolised as follows:

Download Original Figure

These concepts can now be applied in any of the 18 categories of Table 4, using the Force Levels and their appropriate symbolic borders (see p.75). The concepts loud and quiet, if placed at the Causation Level would mean to sound (tr.)/to silence; light and dark placed in this category would mean to illuminate/to darken. These concepts placed in the Feeling category would mean to hear/not to hear and to see/not to see. By way of further example, Haag notes:

In the thought category, the Causation Level itself [III] takes over as the means of expressing intention; to causeto be heard is to say; to cause to see is to show; to cause to know is to inform, such that this class is clearly divided into the two groups of knowing and informing, according to the Level that one uses.

Having established the 37 concepts and their symbols, Haag adds further symbolic combinations and variations, but their complexity and the lack of space within this paper do not permit me to deal with these.

11. Interlude

Thus far we have assembled the following elements which will go towards developing Haag’s ideas in greater detail:

12. Deriving Syntactic Categories from Concepts

As outlined in Maun (2015), Haag is able to demonstrate that some concepts may be derived from others. Thus:

Haag also demonstrates the converse, namely that adverbs can be transformed into verbs. Thus:

Before we examine the question of syntax, we must look at the way in which Haag derives words which will express the relationship of two ideas. These concepts are derived from the first concepts outlined in the system (e.g., proximity and distance). Setting out Haag’s rather dense paragraph on this subject in a more readable way than in the original, we find:

13. Syntax

13.1. Structure

Armed with a vocabulary of Arguments and Functions and a selection of structural words derived from basic concepts, Haag is now able to address the question of syntax.

For the structural order of his propositions, he chooses a linear SVO order. The order of reading is left-to-right. Thus:

[T]he free argument, in which we seek the root of the Function, stands at the beginning; the dependent Argument, in which we seek the effect of the Function, is placed at the end. This construction forms the basis of each conceptual structure. By placing three concepts in this order, we arrive at a thought or expression of perception. The thought ‘Pleasure enhances life’ is entirely determined by three concepts: to take pleasure enhance live in this order, which expresses the causal relationship of the concepts. (p.22)

To represent things and phenomena (and things of unspecified nature) Haag uses the square as a symbol, and for people and animals he uses the circle. Thus the symbolic syntax for A is in B combines a square labelled A, the symbol for in (symbol 7 in his original list) surrounded by a triangle, indicating Level I (State) of this concept, and a further square labelled B. Thus:

Download Original Figure

To symbolise a transitive verb in use (C puts A into B), Haag places the subject first (a circle representing a person labelled C) followed by the concept in at level III (Causation) in an inverted triangle (see pp.69-70 for definitions of border use). The direct object A follows the verb and the adverbial phrase is represented by B. Thus

Download Original Figure

This proposition used at Level IV (C forces A into B) would thus be represented as:

Download Original Figure

13.2. Symbolism and Tenses

Haag uses the following symbols for frequently-occurring words in his examples:

Download Original Figure

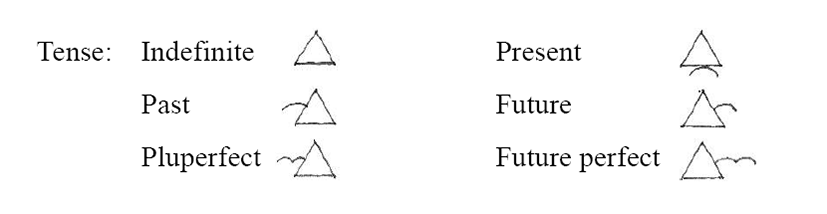
Tense markers are attached to the triangular borders of verbs. The orientation and form of the triangle will of course depend on the Force Level at which the verb is being used:

Download Original Figure

When written symbolically in full, a sentence such as He works so that he becomes rich requires a present tense marker, but as the time is actually unspecified, an abbreviated form with no tense marker is allowed, which conforms with Haag’s ‘Indefinite’ tense marker, i.e., an unadorned triangle.

13.3. Negation

Negation is expressed by a line over the element to be negated. However, the ‘zero’ symbol may be attached.

Download Original Figure

13.4. Relative Clauses

These are attached to Arguments. Haag recognises that a relative clause is, in fact, a full proposition which has been downgraded. Thus, The cat catches the mouse which is in the field is initially analysed as The catcatchesthe mouse [The mouse is in the field]. The relative clause itself is separated from the main clause by the use of square brackets. Within the relative clause, the anaphoric element (i.e., the relative pronoun) is represented by a vertical straight line. Thus, the above sentence becomes, symbolically:

Download Original Figure

Here the circles represent living beings and the square symbol a natural phenomenon (space). The Z represents the category ‘Zoological’, and N stands for ‘Nature’. The symbols > and < represent ‘large’ and ‘small’. These adjectives are not specified in the surface structure of the sentence in Haag’s prose text, but the symbols serve to clarify the relationship of cat and mouse. Later Haag shows how a relative clause such as The cat [which is large] can be further reduced to become The large cat.

13.5. Adverbial Clauses

Haag offers examples of adverbial clauses. Both main and subordinate clauses are normally placed within round brackets (as opposed to square ones used for relative clauses), but the brackets round the main clause may be dropped. In the example below, the symbol for behind at Force Level I is modified by the addition ‘T’ (time) to mean after. The sentence thus means I come after he writes.

Download Original Figure

14. Critique of Haag: A Man of His Time

In critiquing Haag’s system, it must be borne in mind, firstly, that it is only a Versuch, an outline, a mere 83 pages of ideas, and, as Haag stresses, it is theoretical, not practical. Wilkins (1668) thought that his own 300-page Essay was insufficient to define a universal language, but there is a difference between Wilkins and Haag. George Dalgarno criticised Wilkins for failing to reduce his system to absolute primes. Haag, however, has successfully done this, giving a sound outline which may only require some extension or reorganisation.

On the other hand, Haag, was bound by history and by the ideas prevalent at the time (1902). He did not have the benefit of the further century of practical and theoretical work on languages and linguistics which we enjoy today. We shall therefore examine the negative aspects of his work with a certain degree of tolerance before going on to examine the positive side and his important contribution to symbolic language, including a modern Real Character.

On the other hand, Haag, was bound by history and by the ideas prevalent at the time (1902). He did not have the benefit of the further century of practical and theoretical work on languages and linguistics which we enjoy today. We shall therefore examine the negative aspects of his work with a certain degree of tolerance before going on to examine the positive side and his important contribution to symbolic language, including a modern Real Character.

Unlike many previous writers, Haag does not begin his attempt to create a symbolic language by analysing the world into categories. Where the ‘language projectors’ of the 17th century and later writers produced extensive lists of words (mainly nouns), Haag prefers to leave such categorisation alone while he concentrates on semantic primes and ‘logical’ structure. As we have seen above, his use of ‘fields’, to which Verhalten may be applied at various levels, provides a limited range of tangible concepts, e.g., ‘inside’ can give the noun ‘claw’ in the Mechanical field, and in the field of Space can give the noun ‘door’. However, when it comes to symbolising concepts such as ‘cat’ or ‘mouse’, the system goes no lower than the level of ‘biological entity’, and Haag is obliged to write the name of the animal below the symbol. This is clearly a shortcoming, as a nominal designation in written form must appear in some natural language, not in symbolic form. The same is true of most verbs. ‘Wrote’ is symbolised only as a ‘cultural act’ with the German word schrieb written below it.

In his introduction Haag states: ‘We shall see how far the conceptual content common to all human languages can be expressed’. Haag makes the basic assumption here that conceptual content is common to all human languages. While we shall find much to commend his analysis of perceptual and semantic primes, it is evident that languages use these primes in different ways.

Having picked out the vertical and horizontal perceptual axes as the basis for his system, Haag now has a ‘currency’ of units such as ‘near’, ‘far’, ‘in’, ‘on’, etc. However, even Standard European languages do not use these units in exactly the same way. In English, a key may be said to be inthe door. In French, it is sur la porte (on the door). In German, no preposition is used. Instead the verb stecken is used and no mention of place is required: Der Schlüssel steckt (roughly, The key projects). Batchelor & Offord (1982) devote no less than 26 pages of their book to differences between French and English usage of prepositions, and Pinker (2007) points out that while most perceptual distinctions are binary (e.g., here v. there), the distinction is relative, not absolute, and some languages such as Spanish make a three-way distinction between ‘near me’, ‘far from me’, and ‘in between’. Tlingit, a language spoken in the Yukon, has a four-way distinction, adding ‘very far from me’. Haag’s alleged primes are thus very far from being ‘conceptual content common to all human languages’.

In the field of syntax, functional order certainly isn’t universal. Haag’s SVO order within the proposition is very European. A Japanese user of Haag’s system would be obliged to read first the Subject, then go to the end of the sentence to read the Object and then go to the middle to find the Verb, since Japanese is an SOV language. As Haag was a speaker of Turkish, he would have known that that language also uses an SOV order.

Speakers of Celtic languages (Welsh, Scots Gaelic, Erse, Breton) would have to start with the Verb, since these languages use the VSO order. Very few languages use an OSV order, but if Haag’s system were to be ‘universal’, then it should have been capable of accommodating such languages. Clearly it isn’t, at least, in its present form.

Even symbolic languages do not necessarily use an Argument-Function arrangement, corresponding to Haag’s SVO order. In symbolic logic, Functions precede Arguments. Thus A is x is expressed as x [A]. Haag’s syntactic system thus flies in the face of both natural and symbolic languages. His description of his system as being built auf logischer Grundlage (‘on a logical basis’) is not strictly true. Its structure, working from perceptual and semantic primes to the symbolic representation of propositions is, at best, systematic, not logical.

Similarly Haag’s tense system (indefinite [i.e., generic present] – present – past – pluperfect – future – future perfect) is not based on logic, but corresponds neatly to that of Standard European languages, e.g., French or German, but is inadequate for the representation of more ‘exotic’ languages, i.e., those outside the well-known European languages of the time. Deutscher (2010) cites the Matses language, spoken along the Jivari river, a tributary of the Amazon, by about 2,500 speakers. In this language the temporal foci of tenses are widely different from those of European languages. Thus past tenses are chosen depending on whether the event is seen in as being in the recent past (up to a month ago), in the distant past, (roughly from a month to fifty years ago) or remote past (more than fifty years ago).

This is not to say that Haag’s system is incapable of making such distinctions of tense and evidentiality, just as European natural languages can do so. Deutscher (2010) notes that the Matses distinctions can be handled in English by such circumlocutory expressions as ‘I saw with my own eyes a short time ago that …’, ‘I inferred a long time ago that …’, ‘I guessed a very long time ago’, and so on.

On the other hand, where Haag’s system (in the form given) has insufficient means to express such meanings through the verb, in some cases it forces the writer (this is a pasigraphy, remember) to give information which for writers of some languages would not be necessary. Thus Haag requires that tense be indicated on the symbol for the verb, but there are languages in which tense is not indicated, e.g., Mandarin, Vietnamese, and Samoan (Crystal 1987).

Thus Haag’s statement ‘We shall see how far the conceptual content common to all human languages can be expressed’ is both too ambitious and theoretically unsound, since it assumes that there is ‘conceptual content common to all languages’. This in part derives from the tenets of the time at which he was writing and his own studies. The historical relationships of languages (particularly of the Indo-European group) showed that similar grammatical categories seemed to be assignable (sometimes incorrectly), much on the models of the Latin grammars of Donatus and Priscian, and the influence of the Port-Royal grammarians with their aim of revealing ‘the unity of grammar underlying the separate grammars of different languages’ (Robins 1967) was long-lasting.

At the time (1902), of course, serious data-driven research into languages other than those of the Indo-European group was in its infancy (Powell’s classification of Amerindian languages was only published in 1891), and the possibility that languages could exhibit non-European concepts and syntax and non-European grammatical categories had barely dawned on linguists. The era of descriptive as opposed to historical linguistics was yet to come.

Since Haag’s era, the concept of ‘universals’ has experienced both good and bad times. In the era of Sapir and Whorf the general belief was that languages could vary infinitely, i.e., there were no universals, and that the language that one spoke influenced the way that one saw the world, e.g., Sapir (1921) and Whorf (1941). The 1960s saw research into a wider field of languages which provided evidence of commonality, e.g., formal universals (e.g., patterns of word order) and substantive universals (e.g., syntactic or phonological categories) (Greenberg 1963). This was considered to be evidence for what Chomsky calls Universal Grammar. More recently, however, Evans & Levinson (2009) have shown that there are very few alleged universals which appear in all languages, and that the few recurring patterns which are found are better seen as ‘stable engineering solutions satisfying multiple design constraints, reflecting cultural-historical factors and the constraints of human cognition.’ Deutscher (2010) gives further support to the notion that some supposedly universal perceptions, such as colour, are, in fact, partly constrained by culture and language.

Haag’s attempt, therefore, to find ‘the conceptual content common to all human languages’ was doomed to failure from the start, but he was in part a victim of historical ideas and in part a man born before his time. Only later would ideas appear which reflected Haag’s thinking. Until now, he has never received acknowledgement, because of the obscurity of his work, which (a) was published in a booklet, not in an accessible academic journal, and (b) was written in German, rather than in French or English, the academic languages of the time.

15. Haag Renewed: Modern Linguistics

16. Haag and a Modern ‘Real Character’

The notion of a modern digital ‘Real Character’ has been discussed in Maun (2013, 2015). A ‘Real Character’ (hereafter, RC) is a pasigraphy, a symbolic language meant only to be read, not pronounced. The type of system outlined in the two papers mentioned above involves icons, indices, and symbols, with syntactic function being indicated by position (place-value). Such a system has no fixed word order and the glyphs (characters) can be read in the order natural to a native speaker of any given language. For further details, see the two papers in question.

17. Conclusions

Karl Haag’s little book Versucheiner graphischen Sprache auf logischer Grundlage contains a wealth of insight which pre-dates modern research and has unfortunately been ignored, forgotten, or neglected. His aim was not to create a new artificial, symbolic language, but to demonstrate the logical basis on which a pasigraphy might be created, such that meaning would be deducible from form.

Haag deserves credit and his insightful system calls for closer examination and development, particularly by those whose interest lies in artificial languages, universal linguistic systems, and Real Character. Haag’s name does not appear in any of the major surveys of constructed languages. The time has come for him to be included in any further major work resembling those of Couturat & Leau (1903) or Okrent (2009).

Perhaps Haag deserves an epitaph that reflects his concepts and his relevance to the researchers of today. I would suggest:

Haag’s work is not yet over.