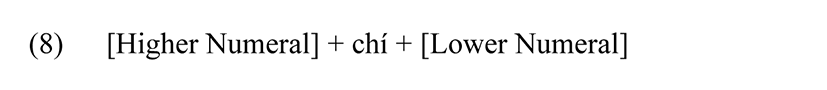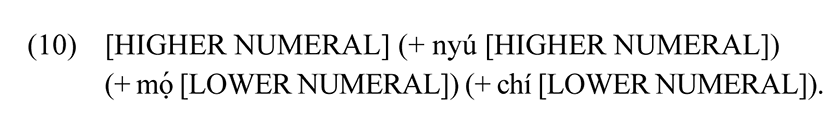1. The Concept of a Numeral System
A numeral system comprises a language’s counting words and the rules governing their formation (Trask 1997). Hammarström (2010) describes numerals as conventional spoken forms that denote exact quantities across object types and social contexts, shared by the entire speech community. Numerals function as cardinals, ordinals, nominals, and sequence markers (Corver et al. 2007), and their recursive morphology can in principle generate infinite values (Booij 2010).
Cross-linguistically, numeral systems are self-contained yet systematic components of grammar (Hurford 1999), structured around base values and operations such as addition and multiplication (Welmers 1974). While many emerge from embodied practices like finger-counting, others extend into abstract domains of measure and time (Payne 1997, Omachonu 2011). This study describes the morphological structure of the Ígálâ numeral system and situates it within broader typologies. As a West Benue-Congo language closely related to Yoruba and Itsekiri (Akinkugbe 1976, Capo 1989), Ígálâ exemplifies both a coherent internal logic and the cultural reasoning encoded in number words.
2. A Cross-Linguistic Exploration of Numeral Systems
Cross-linguistic research shows both diversity and convergence in numeral systems, which encode arithmetic operations, morphosyntax, and cultural conventions. In West Africa, Welmers (1974) highlights multiplicative constructions in Akan, where ńná “and” marks addition, and the highly vigesimal Yoruba system, which combines additive, subtractive, and multiplicative strategies (e.g., seventy-five = four twenties minus five), with higher bases such as 200 and 400. Comparable strategies occur elsewhere: French retains vigesimal remnants (quatre-vingt-dix ‘90’), Latin employs subtraction (undecim ‘11’), Yukatek Maya builds on powers of twenty, and Nuuchahnulth mixes decimal and vigesimal forms while allowing numeral incorporation into verbs. Typological surveys (Hurford 1975, Gvozdanović 1999, Haspelmath et al. 2005, Stonham 2007) show base numerals (10, 20, 60) as universal anchors shaped by cognition and culture. Against this backdrop, Ígálâ stands out for its coherent vigesimal-multiplicative logic, where base units, operations, and morphosyntax form an integrated system, enriching both West African typology and the comparative study of numerical cognition.
Yakub et al. (2021) argue that linguistic description must attend to the internal organization of categories if their communicative force is to be understood. Comrie (2020), in reassessing Greenberg’s claims about numeral systems, reinforces this point by showing that while descending order is widespread, other languages display ascending (Khmer), mixed (German), and vigesimal (Welsh, Breton, French) patterns, each reflecting its own structural logic. Alphonce (2023) adds that such logics are vulnerable to language contact, as seen in the replacement of Alagwa and Burunge numerals by Swahili, which undermines intergenerational transmission. Across these studies, the principle is clear: crosslinguistic comparison must rest on the structural and functional specificities of linguistic categories, even when they are pressured by dominant lingua francas.
Ígálâ is a West Benue Congo language spoken majorly in Kogi State, Nigeria by the Igala ethnic group (Ejeba 2020). Earlier works on numerals in the language (Etu 1999, Ocheja 2001) emphasize lexical reform over structural analysis, differing mainly on the form for ‘100’ (ólíú vs. íchányí). Both overlook the vigesimal logic of the system, treating numerals as static items rather than constructions of addition, multiplication, and subtraction, a concern noted by Ekundayo (1971) and Welmers (1974). Omachonu (2011) advocates decimal reform, claiming the system “did not go beyond one thousand” (2011: 84), a ceiling inconsistent with evidence that vigesimal systems extend much higher (Hurford 1975, Haspelmath et al. 2005). While reflecting modernization concerns, such approaches risk obscuring the coherence of the indigenous system. The present study therefore offers a descriptive account of Ígálâ numerals, analyzing their structural strategies and situating them within cross-linguistic typologies (cf. Gvozdanović 1999, Stonham 2007).
Data for this study were obtained from naturally occurring speech events, supplemented by native-speaker intuition. The researcher, a native speaker of the Dekina dialect of Ígálâ, provided direct linguistic access and internal validation. Examples are presented in tabular format and analyzed through morpheme-by-morpheme glossing, in keeping with the Leipzig Convention for interlinear glossing (Max Planck Institute for Evolutionary Anthropology 2015). Glossing prioritizes morphosyntactic structure over phonological realization. Orthographic conventions follow Miachi and Armstrong (1986), with subsequent modifications proposed in Ejeba (2016). Tone is represented as high (´), low (`), and mid (unmarked). The study adopts a descriptive methodology, providing an overview of the Ígálâ numeral system and examining its morphological and grammatical strategies for encoding numerical relations.
3. The Ígálâ Numeral System
As noted in Section 2, numeral systems vary cross-linguistically in base structures and grammatical strategies. In traditional Ígálâ society, where counting needs were modest, devices such as finger-counting, twigs, kola nuts, or cowries sufficed. Larger quantities were often expressed metaphorically, as in ìlẹ̀ fíá tẹ́ “a mammoth crowd,” literally “the world scattered in place,” ùjẹnwu lọ̀ ómi lọ̀ ẹ̀kẹ̀tẹ̀ “more than enough food,” literally “food rained water rained and sand,” or ọ́kọ́ gwúdọ gwùdọ “an exceedingly large sum of money,” literally “nonsense nonsense money.”
Such strategies met the needs of a subsistence economy, but modern contexts demand greater numerical precision. This raises a typological question: is the Ígálâ system merely a rudimentary tool for basic arithmetic, or a structurally complex system that integrates decimal and vigesimal logics? This study answers by presenting a paradigm of Ígálâ numerals from zero to indefinitely large values, tracing additive, multiplicative, and subtractive strategies, examining borrowing, and situating the system within broader cognitive and typological frameworks. The analysis shows the system to be not only arithmetically robust but also structurally coherent and culturally significant.
Ígálâ numerals are organized through the interplay of additive, multiplicative, and subtractive principles, with base-10 and base-20 interacting in systematic ways. Table 1 presents the paradigm from 0 to 1,000 (and beyond), illustrating both morphological composition and semantic logic.
The Ígálâ numeral system follows a quasi-decimal pattern from 1–19, with values above 10 formed additively (e.g., ẹ̀gwáǒkâ ‘10 + 1’). From 20, it shifts to a vigesimal base (ọ̀gbọ̀mọ́èjì ‘20 × 2 = 40’), while a quinquagenary element (ólí ‘50’) introduces a hybrid vigesimal–quinary structure. Lexicalized forms for single units (ógwú ‘20,’ óje ‘50’) differ from the multiplicative bases (ọ̀gbọ̀ ‘20,’ ólí ‘50’), showing functional specialization; thus, 100 is expressed as ólímọ́èjì ‘50 × 2.’ Numerals beyond 1,000 extend recursively through addition and multiplication (e.g., íchámûnyúọ̀gwáọ́kọ́ ‘800 + 200’), reflecting structural economy and cultural arithmetic ingenuity.
The Ígálâ numeral system comprises distinct lexical items for the numbers zero through ten, which serve as the foundational counting units as in (1).
Beyond these basic units, Ígálâ employs specialized lexical forms that serve as higher counting anchors as illustrated in (2).
These lexical bases form the backbone of the Ígálâ numeral system. The morpheme ọ́kọ́ “money, unit of value” grammaticalized from trade and commercial contexts into general counting, while úlú “four hundred” originates from agrarian usage, literally meaning “seed” and subsequently extended to countable large quantities. Higher numerals are then systematically constructed through functional morphemes that encode arithmetic operations, producing a fully productive number grammar as shown in (3).
The discussion in Sections 3.2–3.4 will therefore demonstrate how lexical anchors and grammatical operators interact to yield additive, multiplicative, and subtractive constructions, while further situating these processes within the broader dynamics of borrowing and contact that characterize the modern Ígálâ numeral system.
Additive constructions in Ígálâ operate across three structural zones: (i) simple juxtaposition up to nineteen, (ii) templatic addition with ny(ú)òké(mọ́)/ny(ú)ọ́wọ́(mọ́) for units following higher bases, and (iii) free addition with nyú beyond nineteen.
Numerals from eleven to nineteen are formed by directly combining ẹ̀gwá ‘10’ with a unit. Alternatively, these values may also be expressed through templatic addition, reflecting the treatment of 1–9 as units within the quasi-decimal structure (4).
This direct juxtaposition is confined to the first cycle of addition but reappears in forms such as ógw(ú)ẹ̀gwá ‘30,’ where it functions as an idiomatic, lexicalized choice. By contrast, the templatic form ógwúny(ú)òkém(ọ́)ẹ̀gwá (‘20 + 10 units’) represents a more transparent, compositional strategy.
From twenty upward, additive constructions require the ny(ú)òké(mọ́) or ny(ú)ọ́wọ́(mọ́) template, the latter metaphorically invoking fingers as counting units. With ọ́wọ́ “one,” the morpheme mọ́ is omitted, giving ny(ú)òké or ny(ú)ọ́wọ́(ǒ)kâ, as shown in (5).
For numerals above one, the full template with mọ́ is obligatory, as illustrated in (6).
Thus, òké/ọ́wọ́ anchor lower numerals as atomic units, giving way to the bare additive nyú as the principal mechanism for constructing higher numbers.
Multiplication in Ígálâ is expressed through the morpheme mọ́ “times” and by templatic strategies at various base thresholds. These strategies extend the system from single units up to billions and beyond. Multiplicative productivity is bounded at each base, reflecting both cognitive economy and cultural arithmetic conventions.
At the lowest tier, multiplication is expressed by the template òkémọ́ X (‘1×X’), where òké “unit” functions as the immutable base and numerals 1–19 serve as multipliers. Within this range, mọ́ merely marks the pattern and signals the multiplicative structure without producing additional semantic content. Multiplication in Base-1 extends from 1 up to 19 and terminates; attempts to extend it to higher numerals (e.g., ẹ̀gwá mọ́ èjì = 10 × 2) are ungrammatical, illustrating the first structural ceiling in the system (Table 2).
This blocking principle motivates the shift to Base-20 (ọ̀gbọ̀) for higher numerals.
Beyond 19, larger numerals are constructed using Base-20 (ọ̀gbọ̀) and Base-50 (ólí) templates, supplemented by additive blends and lexical anchors. Base-20 multiplication (ọ̀gbọ̀mọ́ X) is productive up to 380 (20×19), the vigesimal optimum, which marks the structural ceiling of regular vigesimal computation. Additive constructions fill intermediate gaps, e.g., 30 = ógwú ẹ̀gwá, 70 = ọ̀gbọ̀mọ́ ẹ̀ta ẹ̀gwá.
Certain numerals are lexicalized: 50 = óje, 200 = ọ̀gwáọ́kọ, and 400 = úlúọ́kọ, with 200 also appearing transparently as ọ̀gbọ̀mọ́ẹ̀gwá (20 × 10). From 400 onward, Base-50 multiplication (ólímọ́ X) extends up to 950 (50 × 19), mirroring the vigesimal optimum, but it competes with vigesimal templates, additive blends, and lexical forms. Lexical forms dominate conventional usage, while templates provide arithmetically transparent alternatives (Table 3).
At the threshold of the thousands, Ígálâ reactivates explicit mọ́-based multiplication, which had receded in the mid-range cycles. For example, 2,000 is expressed as íchámû nyú ọ̀gwáọ́kọmọ́ èjì (1,000 × 2), and 19,000 as íchámû nyú ọ̀gwáọ́kọmọ́ ẹ̀gwáẹ̀lá (1,000 × 19). Here, the multiplicative marker mọ́ resumes its full arithmetic function, contrasting with lexical anchors and blends in mid-range numerals.
The vigesimal optimum continues to function as a structural ceiling in the Ígálâ numeral system, with mọ́-based multiplication productive only up to 19,000. Beyond this point, the system shifts from overt mọ́ marking to a strategy of juxtaposing free numerals and employing recursive compounding. For instance, 20,000 is expressed as íchámû nyú ọ̀gwáọ́kọ ógwú (1,000 × 20), while 1,000,000 is formed as íchámû nyú ọ̀gwáọ́kọ íchámû nyú ọ̀gwáọ́kọ (1,000 × 1,000), illustrating how higher numbers are systematically generated without extending the explicit multiplicative marker beyond the vigesimal threshold.
This recursive architecture allows indefinite extension: higher numerals are built by stacking lower anchors in strict descending order, with lexicalization, blending, and template strategies providing systematic, complementary mechanisms (Table 4).
Building on the additive and multiplicative architecture, subtraction in Ígálâ is structurally simpler but functionally narrower, largely restricted to monetary and transactional contexts. The key marker is the morpheme chí “pluck,” which conceptualizes subtraction as the removal of a part from a whole. Its fixed syntactic template is:
Subtraction ensures clarity and structural transparency, as illustrated in (9).
Subtractive constructions are morphologically uniform and allow flexible combinations of minuends and subtrahends. However, they are cognitively more demanding than addition or multiplication, since the base must first be computed (e.g., 100 as 20×5) before subtraction is applied. Communicatively, the unpredictability of subtrahends further limits routine use.
Notably, subtraction does not conform to the vigesimal optimum (19) that governs productive multiplication. There is no ceiling on the size of either minuend or subtrahend; any higher numeral can be reduced by any smaller numeral. This contrasts with addition and multiplication, where the vigesimal optimum constrains productive combinations. Despite this, subtraction fully respects the hierarchical top-down ordering: the minuend (higher numeral) always precedes the subtrahend (lower numeral), consistent with the structural transparency of the Ígálâ numeral system.
Conceptually, the minuend precedes the subtrahend, in contrast to Latin-style ‘one from ten’ constructions, reflecting a distinct, transparent mapping of subtractive reasoning that aligns with the hierarchical and metrical architecture of the numeral system.
A defining feature of the Ígálâ numeral system is the vigesimal optimum (19), which sets a ceiling for productive multiplication across all arithmetic cycles. At the unit level, nineteen marks the upper limit of simple lexical items (ẹ̀gwáẹ̀lá = 19). In the vigesimal cycle, multiplication extends up to 20 × 19 = 380 (ọ̀gbọ̀mọ́ ẹ̀gwáẹ̀lá), while in the quinquagenary cycle, it reaches 50 × 19 = 950 (ólímọ́ẹ̀gwáẹ̀lá). In the thousands, mọ́-based multiplication operates from 1,000 × 2 up to 1,000 × 19 = 19,000 (íchámû nyú ọ̀gwáọ́kọmọ́ ẹ̀gwáẹ̀lá). Beyond this ceiling, multiplication via mọ́ is blocked, and higher numerals are expressed through nyú-mediated addition, lexical blends, or juxtaposition, as in 20,000 = íchámûnyúọ̀gwáọ́kọ ógwú or 1,000,000 = íchámûnyúọ̀gwáọ́kọ íchámûnyúọ̀gwáọ́kọ, illustrating recursive stacking of anchors.
While the vigesimal optimum governs multiplication, subtraction operates independently. Any higher numeral can serve as minuend or subtrahend without restriction by 19, highlighting that subtraction is a specialized operator rather than a fully integrated arithmetic cycle.
This study confirms Comrie’s (2020) claim that Greenberg’s ordering universals should be treated as tendencies rather than absolutes. Crosslinguistically, languages such as Sakalava Malagasy and Insular Celtic show ordered shifts at structural cut-off points (e.g., 20, 60, 100), demonstrating that high-before-low ordering, though globally dominant, is not inviolable. Ígálâ, however, provides a counterweight within this spectrum: it exemplifies a strict descending system in which higher numerals consistently precede lower ones, without cut-off reversals or mixed strategies.
Grounded in the vigesimal optimum (19), Ígálâ organizes its numerals through a hierarchical template with dual operators: nyú marking additive or juxtaposed combinations and mọ́ marking multiplicative scaling. Additive forms like ẹ̀gwá(ǒ)kâ ‘11’ (10 + 1) contrast with the ungrammatical reversed ǒkâẹ̀gwá. Multiplicative constructions (ógwúẹ̀gwá ‘30’ = 20 + 10; úlúọ̀gwá ‘600’ = 400 + 200) maintain the descending order that Celtic systems, by contrast, relax after 20. Even subtraction (ọ̀gbọ̀m(ọ́)ẹ̀lú chí ẹ̀lú ‘95’ = (20 × 5) − 5) adheres to the same hierarchy, where Malagasy often permits alternative structuring.
Large numerals extend the same logic. Multiplication is capped by the vigesimal ceiling, after which juxtaposition applies, as in íchámû nyú ọ̀gwáọ́kọmọ́ ẹ̀gwáẹ̀lá ‘19,000’ (1,000 + 20 × 19) and íchámû nyú ọ̀gwáọ́kọ ógwú ‘21,000’ (1,000 + 20,000). The generalized Ígálâ template can be schematized as follows:
By maintaining recursive, transparent, and typologically coherent structures across all operations, Ígálâ buttresses Comrie’s crosslinguistic claim foreshadowed in Rutkowski (2003): even where universals admit exceptions, the high-before-low principle exerts strong gravitational force on numeral systems. Ígálâ thus provides a ‘purist’ case that sharpens our understanding of how robust tendencies manifest alongside controlled variability in the world’s numeral architectures.
Borrowed numerals in Ígálâ reflect layered sociohistorical contact, including British colonial administration, Hausa trade, and contemporary English influence. These forms are functionally restricted, appearing almost exclusively in monetary contexts and rarely extending to general counting. From British currency, the term ípámû “pound” persisted well beyond Nigeria’s 1973 reform, with constructions like ípámû mọ́ ẹ̀lú (“pound times five” = ₦10) showing how colonial-era forms were arithmetically adapted to the naira. Hausa influence contributed èjìka (from jẹka, “bag”) for ₦200, especially in bulk trade (e.g., èjìka mọ́ ẹ̀gwá = ₦2,000). As Oyinloye (2020) notes, loanwords, a universal outcome of language contact, are not simple transfers but are reshaped by the structural preferences of the borrowing language. Beyond phonological accommodation, an Ígálâ calque àkpúlù “sack” appears alongside the Hausa form for “two hundred,” further illustrating this internal logic. More recently, English exerts pressure through code-switching, as urban youth increasingly use “two hundred naira” instead of indigenous èjìka (ǒ)kâ.
Such items exemplify Hammarström’s (2010) notion of a restricted numeral system: domain-specific, communicatively efficient, but structurally peripheral. While borrowed forms enhance clarity in monetary discourse, their spread threatens the integrity of Ígálâ’s indigenous numeral architecture. In this respect, Ígálâ resonates with broader typological concerns raised by Alphonce (2023) on the Cushitic languages Alagwa and Burunge, where Swahili contact has progressively displaced native numeral systems and curtailed intergenerational transmission. The difference lies in scale: whereas Alagwa and Burunge face wholesale replacement, Ígálâ demonstrates a reasonable containment strategy in which borrowed forms are integrated and functionally narrowed, though not without long-term risks.
4. Conclusion
This study has shown that the Ígálâ numeral system, though displaying a limited decimal arrangement in the lower range (‘one’ to ‘nineteen’), is best characterised as vigesimal. Counting in twenties is the generative base, with fifties reducible to twenties but not the reverse, confirming Omachonu’s (2011) analysis. Within this framework, Ígálâ exemplifies a strict high-before-low ordering: higher numerals consistently precede lower ones across addition, multiplication, subtraction, and large-number constructions. Through the dual operators nyú (additive juxtaposition) and mọ́ (multiplicative scaling), the system maintains recursive and transparent structures. In contrast to systems like Sakalava Malagasy and Insular Celtic, which show ordering reversals at cut-off points, Ígálâ stands as a ‘purist’ case of crosslinguistic tendencies, reinforcing Comrie’s (2020) view of Greenberg’s universals as strong but non-absolute principles.
Borrowed forms from trade and colonial contact exist, but they are peripheral and largely confined to monetary discourse, leaving the core architecture intact. This resilience underscores the adaptability of Ígálâ numerals in accommodating contact-induced items without compromising structural integrity. More broadly, Ígálâ contributes to typological debates by showing how robust ordering principles and vigesimal logic persist even in contact-rich settings. It thus offers a valuable test case for future comparative and diachronic research on numeral systems under conditions of variability and exchange.