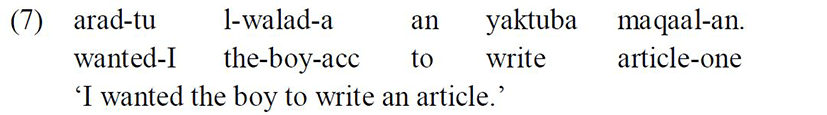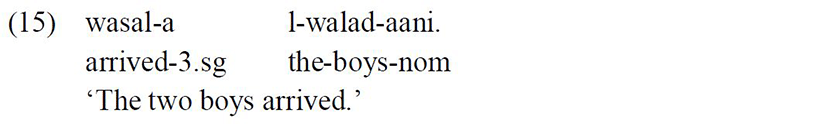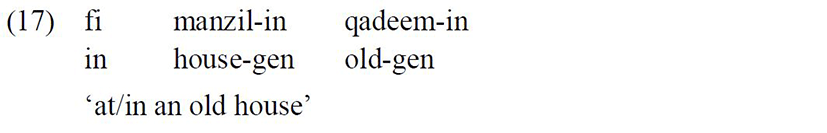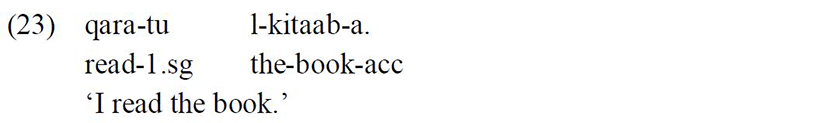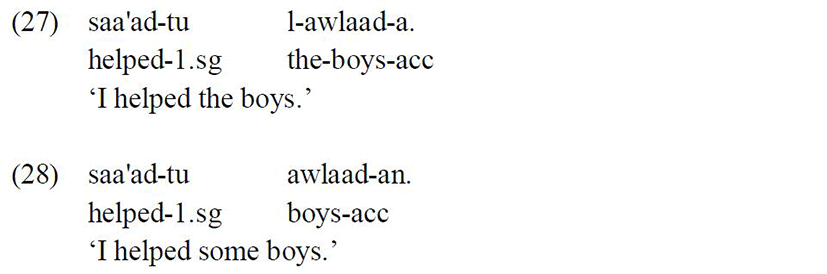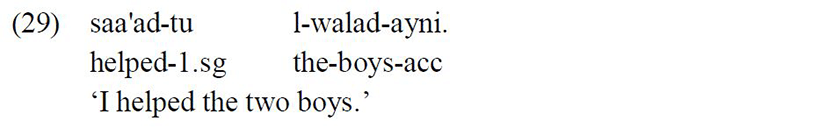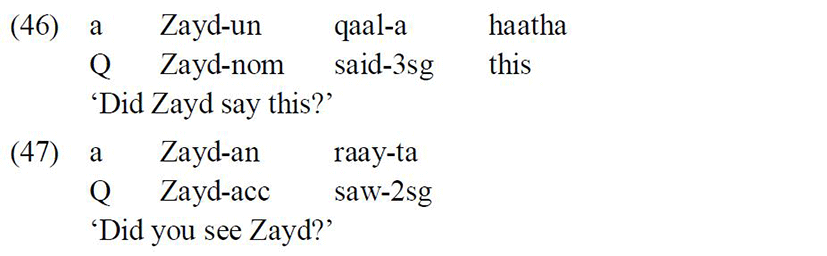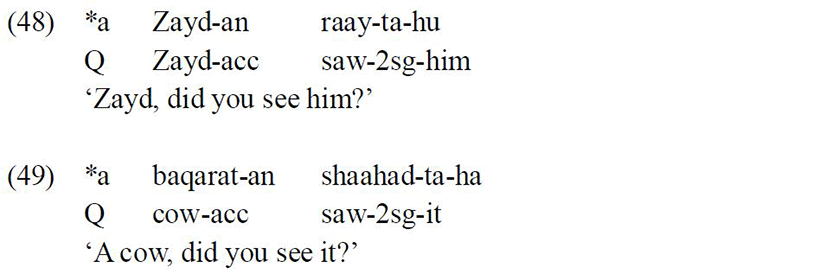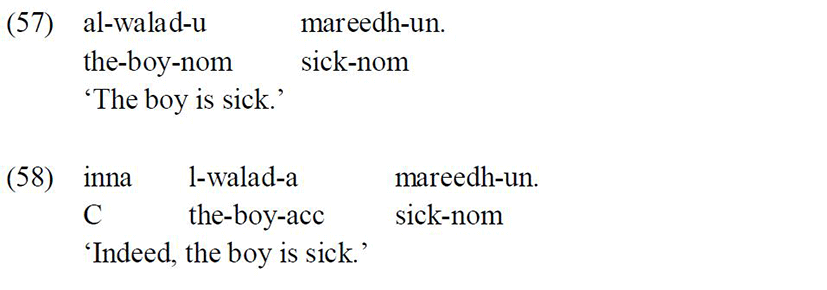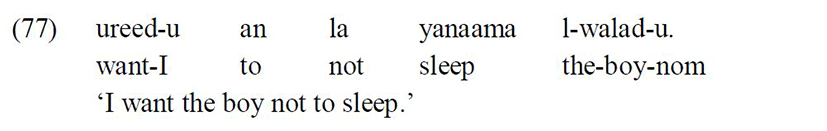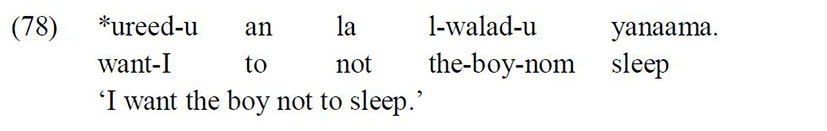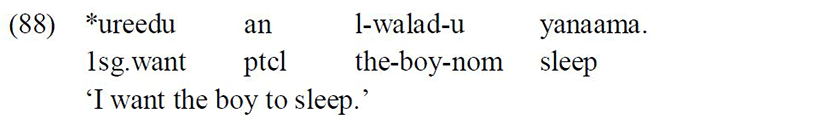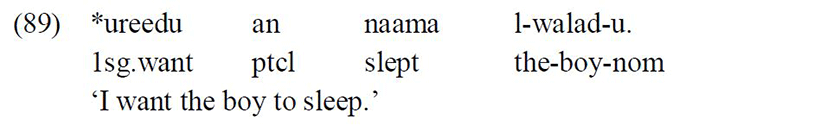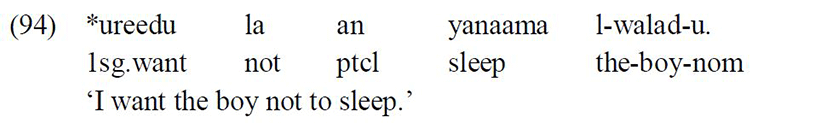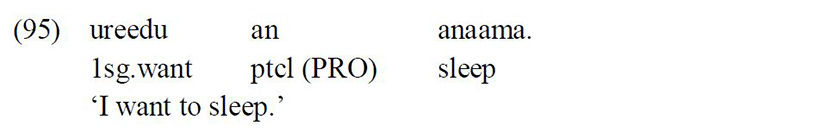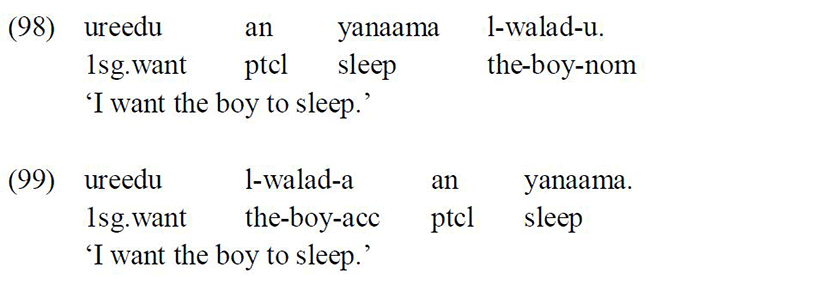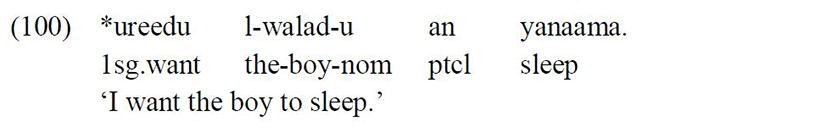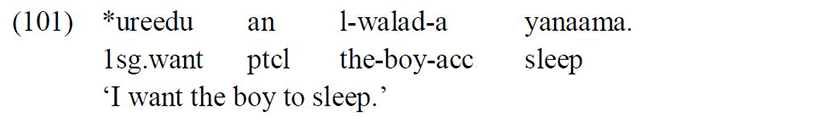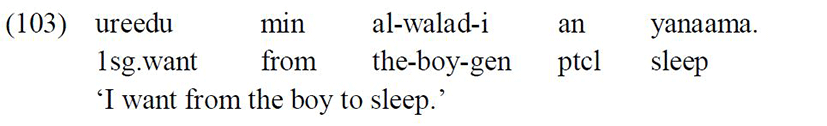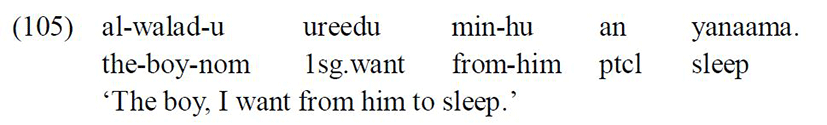1. Introduction
Head-initial languages have the property of what is termed in the literature ‘free inversion’ where the subject can optionally follow the verb (Kotzoglou 2006). In Standard Arabic, the subject can freely precede or follow the verb and in both word orders surfaces with a nominative Case marker (Ouhalla 1994)1:
However, the subject can appear with an accusative Case marker in certain contexts. The first context is when the subject is preceded by a complementiser in matrix as well as embedded clauses:
The examples above show that the subject DP alwalad-a ‘the boy’ appears with an accusative Case marker, whether in the matrix or embedded clause, when preceded by a complementiser (FassiFehri 1993, Benmamoun 2000).
The second context is when the subject is immediately preceded by a negation particle (Benmamoun 2000):
It is to be noticed that the sentence is rendered ungrammatical if the subject DP following the negation particle appears with a nominative Case.
The third context is when the preverbal subject is followed by a tenseless verb in nonfinite clauses. For example, in embedded subjunctive clauses in Standard Arabic the verb lacks tense and the preverbal subject of the embedded non-finite verb surfaces with an accusative Case:
However, if the embedded subject surfaces postverbally, it appears with a nominative Case:
The examples discussed so far show that the preverbal subject in Standard Arabic can surface with an accusative Case marker in certain contexts.
The phenomenon of having accusative subjects in Standard Arabic has not been investigated and accounted for in recent literature due to two main reasons. The first is that some linguists still believe in the traditional theorem that this language cannot have preverbal subjects in the first place, and any preverbal DP is assumed to be a topic. In the second section of this paper, I examine this claim and conclude that subjects and topics are distributionally and structurally different; and that not every preverbal DP is a topic (Rizzi 2004). Standard Arabic can have preverbal subjects as well as topics.
The second reason for not examining accusative subjects in this language in recent literature is the assumption that all lexical categories can assign Case, and this assumption is adopted by modern linguists. For example, complementisers are assumed to assign an accusative Case to a following DP and negation is assumed to assign an accusative Case to a following DP as well (FassiFehri 1993, Benmamoun 2000). Crucially, the DP following the complementiser or the negation particle is not considered a subject in the first place. It is assumed to be a topic since it has left its base-position inside the vP shell.
This paper is divided as follows: the second section of this paper presents a brief typological sketch of the Case system in Standard Arabic. The third section contrasts subjects and topics in this language in order to establish that Standard Arabic can have preverbal subjects as well as preverbal topics. The main argument in this section is that there are topics in this language but it does not mean that every preverbal DP is a topic. Standard Arabic can have preverbal subjects and this is shown in the different syntactic distribution of both subjects and topics.
The fourth section looks at the first context in Standard Arabic where a preverbal subject surfaces with an accusative case marker. This context arises whenever a complementiser in this language chooses to surface. Complementisers in Standard Arabic mandate a strict SV order in their complement and the subject of their complement must be Case-marked accusative. In addition, these complementisers can be null, however their empty position continues to mandate an SV complement with an accusative subject. Moreover, when the subject following the complementiser is topicalised, it must leave behind a pronominal clitic attached to the complementiser.
The fifth section examines another context in which the preverbal subject in Standard Arabic appears with an accusative Case. This context arises when the preverbal subject follows certain sentential negation particles in this language. The negation particle/head la mandates an SV word order of the clause that follows and the Case of the subject that follows this negation head must be accusative.
The sixth section of this paper investigates the context in which the preverbal subject of nonfinite embedded clauses in Standard Arabic surfaces with an accusative Case. These embedded clauses are the subjunctive complements whose verb lacks tense and usually headed by the nonfinite particle an.
In the seventh section, I provide a new analysis to account for these instances of preverbal accusative subjects in Standard Arabic. The new analysis assumes that there are two different positions for the preverbal subject in this language: i) spec-TP, which hosts the grammatical subject; and ii) a higher spec-SubjP, which hosts the subject of predication, along lines discussed in Cardinaletti (2004). Crucially, accusative subjects appear in the spec position of the higher projection SubjP, not spec-TP. I argue that the preverbal subject appears in spec-SubjP with an inherent accusative case.
The last section summarises the main findings and claims discussed throughout the paper.
2. Case System in Standard Arabic
Blake (1994: 1) defines Case as follows: “Case is a system of marking dependent nouns for the type of relationship they bear to their heads. Traditionally the term refers to inflectional marking, and, typically, case marks the relationship of a noun to a verb at the clause level or of a noun to a preposition, postposition or another noun at the phrase level.”
DPs in Standard Arabic are Case-marked in all positions at all times. Case inflection is taken to indicate the syntactic function of the word and its relationship with other lexical items in the sentence (Ryding 2005).
Standard Arabic has three Cases: the nominative, the genitive, and the accusative. Traditionally, each Case is indicated on DPs/NPs by a short vowel that is suffixed to the noun or a modification of a long vowel suffix (Ryding 2005). The main morphological markers cited in the literature are as follows: the nominative Case marker ‘-u’; the genitive Case marker ‘-i’; and the accusative Case marker ‘-a’. However, these markers are not the only morphological manifestation of Case on nouns in Standard Arabic. Case-marked nouns fall into several declensions and inflect for Case in different ways. For example, the Case marker on a definite noun is different from that on an indefinite one, and a Case marker on a dual noun is different from that on a plural one.
In the following sub-sections, I present some of the distributional properties of the three Cases in Standard Arabic. The presentation is not exhaustive, but it covers the majority of occurrences of these Cases in this language.
The DP/NP in Standard Arabic appears with a nominative Case marker when it is a subject or a Topic. Nominative Case can be marked morphologically by four different suffixes: ‘-u’, ‘-un’, ‘-uuna’, and ‘-aani’ (Ryding 2005).
When the noun is singular and preeceded by the definite article ‘al’, it takes the nominative marker ‘-u’:
However, when the noun appears without the definite article ‘al’, it takes the nominative marker ‘-un’:
A regular plural noun (where plurality is indicated by a suffixal marker) usually takes the nominative marker ‘-uuna’ whether it is preceded by the article ‘al’ or not:
On the other hand, the irregular plural noun (where plurality is indicated by an infixal marker or vowel mutation) never takes the nominative marker ‘-uuna’. Instead, it surfaces with the suffix ‘-u’ when preceded by the article ‘al’ and the suffix ‘-un’ when it is not preceded by the article ‘al’:
Furthermore, when the noun is dual, it appears with the nominative marker ‘-aani’:
It is to be noted that in most cases the suffixal marker actually reflects information of more than one category. Therefore, the same suffix can represent Case as well as number, at the same time. Morphological syncretism is a typical inflectional property of Standard Arabic.
The DP/NP in Standard Arabic is Case-marked genitive when it is the object of a preposition, the object of a locative adverb, or the second noun in a construct state construction. The genitive Case markers in this language include the following suffixes: ‘-i’, ‘-in’, ‘-a’, ‘-iina’, and ‘-ayni’ (Ryding 2005).
When the noun is singular and preceded by the definite article ‘al’, it takes the genitive marker ‘-i’:
However, when the noun appears without the article ‘al’, it takes the genitive marker ‘-in’:
In addition, the regular plural noun takes the genitive marker ‘-iina’ whether it is preceded by the article ‘al’ or not:
On the other hand, the irregular plural noun surfaces with the genitive marker ‘-i’ when preceded by the article ‘al’ and the marker ‘-in’ when it lacks the article ‘al’:
Furthermore, when the noun is dual, it appears with the genitive marker ‘-ayni’:
The DP/NP in Standard Arabic surfaces with an accusative Case marker when it is the object of a transitive verb, numbers between 11 and 99, complements of linking verbs, nouns after complementisers, nouns after negation particles, or subjects of nonfinite verbs. Accusative Case can be marked by the following different suffixes: ‘-a’, ‘-an’, ‘-iina’, and ‘-ayni’ (Ryding 2005).
When the noun is singular and preceded by the definite article ‘al’, it takes the accusative marker ‘-a’:
However, when the noun appears without the article ‘al’, it takes the accusative marker ‘-an’:
A regular plural noun takes the accusative marker ‘-iina’ whether it is preceded by the article ‘al’ or not:
However, the irregular plural noun appears with the suffix ‘-a’ when preceded by the definite article ‘al’ and the suffix ‘-an’ when it is not preceded by the article ‘al’:
Furthermore, when the noun is dual, it appears with the accusative marker ‘-ayni’:
3. On Subjects and Topics
Preverbal DPs in Standard Arabic have been often analysed as instances of Topicalisation/CLLD structures. However, I will show that this assumption can be empirically challenged. Subjects and topics have different properties that set them apart (Rizzi 2004). One of the properties of topics in Standard Arabic is that they are necessarily definite, whereas preverbal subjects in this language can be indefinite. However, preverbal indefinite subjects have to be specific (FassiFehri 1993: 28):
Thus, while preverbal subjects in Standard Arabic can be indefinite, topics cannot be indefinite in this language, consequently the ungrammaticality of the examples below when the left-dislocated DP is indefinite (FassiFehri 1993: 29):
It is also argued that preverbal subjects differ from topics in their structural position. Thus, while topics are in the CP domain, subjects are outside this domain and pattern like fronted objects:
Another property that distinguishes subjects from topics in Standard Arabic is their behaviour with negation markers. Negation in Standard Arabic is argued to select a TP in which either the verb is initial (VS order), or a fronted subject/object surfaces preverbally (SV order) (FassiFehri 1993: 30):
On the contrary, topics cannot follow negation markers, as shown by the ungrammaticality of the sentence below:
Moreover, fronted subjects and objects in Standard Arabic can be preceded by a question particle in Yes/No questions (FassiFehri 1993: 31):
However, in Standard Arabic, a question particle cannot precede a topic in Yes/No questions:
Moreover, it is argued (FassiFehri 1993) that pronominals are inherently definite and that pronominal subjects in Standard Arabic do not surface postverbally, therefore the pronominal in the example below must be the subject:
On this basis, one can argue that not every definite preverbal DP is a topic in Standard Arabic. The pronominal DP in the example above is the subject of the sentence, and subjects can actually precede verbs in this language. The above data and arguments clearly show that preverbal DPs in Standard Arabic can be subjects and they differ structurally and distributionally from topics.
4. Accusative Subjects and Complementisers
Complementisers in Standard Arabic mandate a strict SV complement in which the subject DP appears with an accusative Case marker (FassiFehri 1993, Shlonsky 1997). The class of complementisers includes inna, anna, ka’anna, lakenna, layta, andla’alla. When a clause, be it matrix or embedded, is headed by a complementiser, there must be an overt subject following the complementiser and that subject must be Case-marked accusative. Compare the two examples below:
The examples above show that the subject alwalad ‘the boy’ is marked with the accusative Case marker -a when preceded by a complementiser. A nominative subject in this position renders the sentence ungrammatical:
This state of affairs is not exclusive to matrix clauses. Embedded clauses in Standard Arabic must have an SV order with an accusative subject when the embedded clause is headed by a complementiser:
Complementisers in Standard Arabic can also head sentences that lack surface verbs or what classical Arab grammarians dubbed ‘the nominal sentence’ (Ryding 2005). Similarly, the DP following the complementiser surfaces with an accusative Case marker:
In addition, sentences in Standard Arabic can surface with a null complementiser. This assumption can borrow support from the fact that we find the same pattern in these sentences in terms of the strict SV order in the embedded clause as well as the mandatory accusative Case of the subject:
In the two examples above, the embedded clauses show a pattern of word order and Case similar to the ones headed by overt complementisers. Empirical evidence for the existence of a null complementiser heading the embedded clauses above can be seen in the compulsory SV order of these embedded clauses:
In the example above, the embedded clause has a VS word order. The verb of the embedded clause is finite and agrees with its subject. If one denies the existence of a null complementiser heading the embedded clause and mandating a strict SV order of its complement, it would be difficult to explain the ungrammaticality of this sentence. Obviously, this discrepancy can be explained by the fact that there is a null complementiser heading the finite embedded clause and this mandates a strict SV order in the embedded clause following the complementiser.
Another piece of empirical evidence for null complementisers can be detected in the compulsory accusative Case on the subject of the embedded clause:
The two sentences above are ungrammatical, because of the nominative Case on the subject of the embedded clause, suggesting that a preceding null complementiser actually exists, which, in turn, accounts for the accusative Case on the adjacent DP.
The possibility that such embedded clauses are TPs in which the accusative Case on the preverbal subject is assigned by the probe of the matrix verb is ruled out on two grounds. First, we can optionally insert an overt complementiser in these contexts:
Second, adverbial phrases can appear between the matrix verb and the embedded clause (cf. Costa 1997, Cinque 1999, Belletti 2004), suggesting that the verb cannot probe the subject of the embedded clause:
Thus, it is clear that when complementisers in Standard Arabic head a clause or a sentence, the subject of that clause or sentence must carry an accusative Case marker.
5. Accusative Subjects and Negation
Standard Arabic employs a number of particles to denote negation. Among these particles are lam, lan, and la (Ryding 2005). Typically, negation particles can appear in a sentence-initial position followed by the verb:
The negation particles lam and lan cannot be followed by the subject DP (FassiFehri 1993, Benmamoun 2000, Ryding 2005), hence the ungrammaticality of the sentences below:
However, these two negation particles can be preceded by the subject:
It is clear from the examples above that the negation particles lam and lan cannot be followed immediately by the subject. In addition, when the subject appears with these negation particles it surfaces with a nominative Case whether it precedes the negation particle or follows the verb.
However, the negation particle la has another property. Semantically, this particle has two denotations. The first is to negate the occurrence of an action or event (Ryding 2005). In this context, it must be followed by the verb:
In addition, this particle can negate verbs in nonfinite contexts where the subject appears postverbally with a nominative Case:
The subject in nonfinite clauses cannot follow the negation particle:
The examples above show that the negation particle la can be followed by the verb and the Case of the subject that follows that verb must be nominative.
The second denotation of the negation particle la is negating the existence of something (Ryding 2005). In this context, the particle must be followed by the subject, not the verb:
It is to be noticed that verbs cannot follow the negation particle la in this context, hence the ungrammaticality of the sentences below:
In addition, the negation particle la can negate a nominal sentence, i.e., a sentence which lacks a surface verb (Ryding 2005):
The important point in this discussion is that the subject DP that immediately follows the negation particle la always appears with an accusative Case. If the subject DP fails to be Case-marked accusative, the sentence is rendered ungrammatical:
The examples above are all ungrammatical because of the nominative Case marker on the subject DP that follows the negation particle la.
6. Accusative Subjects and Tenselessness
A typical nonfinite context in Standard Arabic where the subject appears with an accusative Case marker is the subjunctive complementation. Before examining the asymmetrical behaviour of subjects in this context, I look at some of the main properties of these clausal complements.
Subjunctive clauses in Standard Arabic are introduced by one of these functional particles: an, kay, li, likay, and hatta (Ryding 2005). These particles will be glossed as ‘ptcl’ throughout this section:
It is to be noticed that the embedded subject cannot intervene between the particle an and the embedded verb, hence the ungrammaticality of the sentence below:
In addition, the verb following the particle an lacks tense (FassiFehri 1993, Benmamoun 2000, Ryding 2005). The tense of the embedded clause is dependent on the matrix clause:
Moreover, the embedded subject that follows the verb in this nonfinite context always appears with a nominative Case, hence the ungrammaticality of the sentence below when the embedded subject surfaces with an accusative Case:
Furthermore, subjunctive complements in Standard Arabic can be negated only by the negation particle la, but not lam or lan, since the latter encode tense and the subjunctive clauses are basically nonfinite:
Also, the negation particle must follow the functional particle an. Any alternative order between these two particles renders the sentence ungrammatical:
Subjunctive complements can be categorised into three types when it comes to subject distribution. The first type is the control structure, in which the subject of the embedded verb is PRO which is referential on the subject of the matrix clause:
The second type is what I call the obviation structure, in which there is always a surface nominative subject following the embedded verb. In this type the subject cannot precede the functional particle, hence the term ‘obviation structure’:
The third type is an ECM-like type in which there is always a surface subject, but this subject can have two different positions either following the embedded verb or preceding the functional particle an:
It is to be noticed that the embedded subject in the two examples above surface with different Case markers: nominative in the first when it follows the embedded verb; and accusative in the second when it precedes the functional particle an.
The accusative Case marker on the embedded subject is obligatory, hence the ungrammaticality of the sentence below when the embedded preverbal subject appears with a nominative Case:
The accusative Case on the embedded preverbal subject cannot be assigned by the functional particle, since this subject cannot follow the functional particle in any context:
Also, the accusative Case cannot be assigned by the matrix verb, since certain categories like adverbial phrases can intervene between the matrix verb and the embedded accusative subject:
Another important point here is that the embedded subject can appear with a genitive Case marker if preceded by a preposition:
The embedded subject can also be topicalised and moved to a sentence-initial position. In this position, the subject surfaces with a nominative Case marker and must leave a pronominal clitic in its base-position:
The genitive subject can also be topicalised, vacating the prepositional phrase to a sentence-initial position, but leaving a pronominal clitic behind:
7. A New Analysis
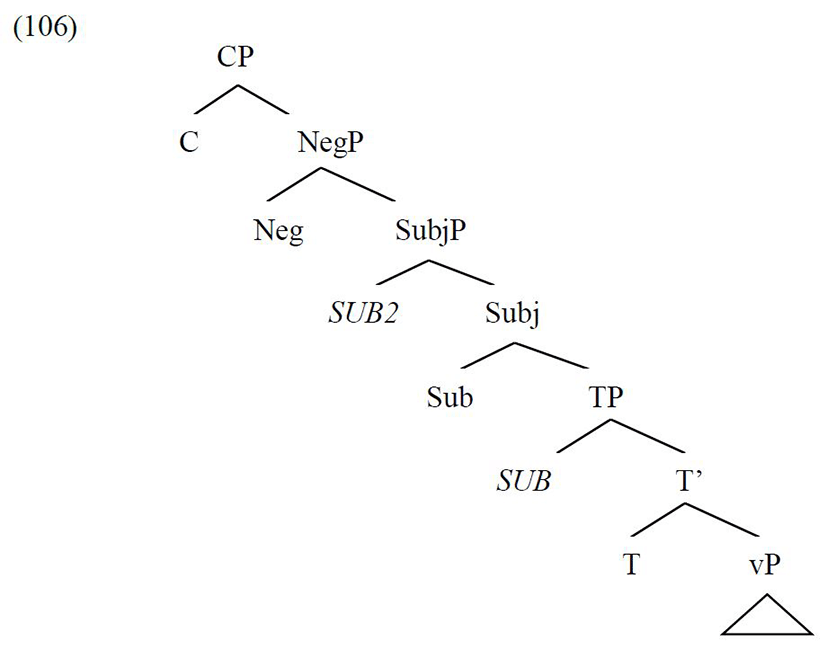
I argue that the accusative subject in the three contexts in Standard Arabic is base-positioned in the specifier position of a projection higher than TP and lower that CP. The new projection can be called SubjP which is a projection that hosts subjects of predication, along lines discussed in Cardinaletti (2004). Crucially, the accusative Case on the subject in spec-SubjP is an inherent Case. I also argue that the specifier position of the TP projection hosts only grammatical nominative subjects that have vacated their base-position inside the vP shell and moved to spec-TP:
The tree diagram above shows that the SubjP projection is positioned below CP and can be preceded by a Neg projection that hosts the sentential negation particle in Standard Arabic. The specifier position of SubjP can host the preverbal accusative subject in the three different contexts investigated in this paper, namely the accusative subject that follows complementisers, the accusative subject that follows negation particles, and the embedded accusative subject that precedes tenseless verbs in nonfinite contexts.
The assumption that accusative subjects are base-positioned and not moved from spec-vP accounts for several issues. First, the dilemma of accounting for how a nominative Case gets overwritten by another accusative Case, assuming that the nominative DP moved from spec-vP to spec-TP (Chomsky 2001, 2005), is explained. The accusative subject has not moved from spec-vP but base-positioned in spec-SubjP, consequently this subject has not been assigned a nominative Case in the first place. Second, the fact that the preverbal subject DP can appear with either a nominative or an accusative Case is explained in terms of availability of syntactic positions, rather than optionality in Case marking. Third, it accounts for the instances where the subject appears with a genitive Case when it follows a preposition, otherwise the nominative subject would be assumed to have merged with a PP on the way from spec-vP to spec-TP and its Case got overwritten and marked genitive, a dubious explanation at best.
8. Conclusions
The phenomenon of having accusative subjects in Standard Arabic has not been investigated and accounted for systematically in recent literature due to two main reasons. The first is that some linguists still believe in the traditional theorem that this language cannot have preverbal subjects in the first place, and any preverbal DP is assumed to be a topic. I have examined this claim and concluded that subjects and topics are distributionally and structurally different; and that not every preverbal DP is a topic. Standard Arabic can have preverbal subjects as well as topics. The second reason is the assumption that all lexical categories can assign Case, and this assumption is adopted by modern linguists. For example, complementisers are assumed to assign an accusative Case to a following DP and negation is assumed to assign an accusative Case to a following DP as well. Crucially, in recent literature the DP following the complementiser or the negation particle is not considered a subject in the first place. It is assumed to be a topic since it has left its base-position inside the vP shell.
In this paper, I argue for a new analysis of preverbal accusative subjects in Standard Arabic in terms of availability of syntactic positions, rather than optionality in Case marking. I argue that the preverbal accusative subject in this language has not moved from spec-vP but base-positioned in spec-SubjP, which is a projection between CP and TP that hosts subjects of predication, along lines discussed in Cardinaletti (2004). Crucially, the accusative Case on the preverbal subject in spec-SubjP is inherent and not assigned by any head.